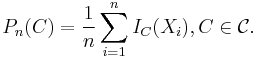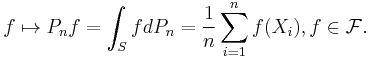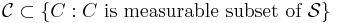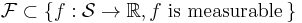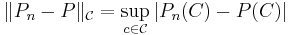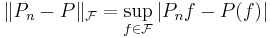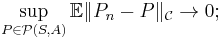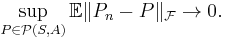Glivenko–Cantelli theorem

Assume that 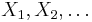$X_1,X_2,\dots$ are independent and identically-distributed random variables in $\mathbb{R}$ with common cumulative distribution function F(x). The empirical distribution function for $X_1,\dots,X_n$ is defined by

$F_n(x)=\frac{1}{n}\sum_{i=1}^n I_{(-\infty,x]}(X_i),$

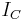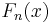where $I_C$ is the indicator function of the set $C$ . For every (fixed) x, $F_n(x)$ is a sequence of random variables which converge to F(x) almost surely by the strong law of large numbers, that is, 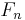$F_n$ converges to F pointwise. Glivenko and Cantelli strengthened this result by proving uniform convergence of 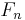$F_n$ to F.

Theorem

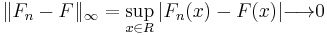$\|F_n - F\|_\infty = \sup_{x\in R} |F_n(x) - F(x)| {\longrightarrow} 0$ almost surely.^[2]

This theorem originates with Valery Glivenko,^[3] and Francesco Cantelli,^[4] in 1933.

Remarks

If 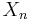$X_n$ is a stationary ergodic sequence, then 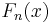$F_n(x)$ converges almost surely to 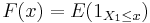$F(x)=E(1_{X_1\le x})$ . The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case.
An even stronger uniform convergence result for the empirical distribution function is available in the form of an extended type of law of the iterated logarithm.^[5] See asymptotic properties of the Empirical distribution function for this and related results.

Empirical measures

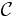One can generalize the empirical distribution function by replacing the set $(-\infty,x]$ by an arbitrary set C from a class of sets $\mathcal{C}$ to obtain an empirical measure indexed by sets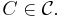 $C \in \mathcal{C}.$

$P_n(C)=\frac{1}{n}\sum_{i=1}^n I_C(X_i), C\in\mathcal{C}.$

Further generalization is the map induced by 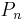$P_n$ on measurable real-valued functions f, which is given by

$f\mapsto P_nf=\int_SfdP_n=\frac{1}{n}\sum_{i=1}^n f(X_i), f\in\mathcal{F}.$

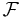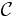Then it becomes an important property of these classes that the strong law of large numbers holds uniformly on $\mathcal{F}$ or $\mathcal{C}$ .

Glivenko–Cantelli class

Consider a set 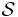$\mathcal{S}$ with a sigma algebra of Borel subsets A and a probability measure P. For a class of subsets,

${\mathcal C}\subset\{C: C \mbox{ is measurable subset of }\mathcal{S}\}$

and a class of functions

$\mathcal{F}\subset\{f:\mathcal{S}\to \mathbb{R}, f \mbox{ is measurable}\,\}$

define random variables

$\|P_n-P\|_{\mathcal C}=\sup_{c\in {\mathcal C}} |P_n(C)-P(C)|$

$\|P_n-P\|_{\mathcal F}=\sup_{f\in {\mathcal F}} |P_nf- P(f)|$

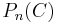where $P_n(C)$ is the empirical measure, 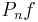$P_n f$ is the corresponding map, and

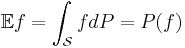$\mathbb{E}f=\int_\mathcal{S} fdP = P (f)$ , assuming that it exists.

Definitions

A class 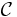$\mathcal C$ is called a Glivenko–Cantelli class (or GC class) with respect to a probability measure P if any of the following equivalent statements is true.

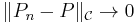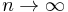1. $\|P_n-P\|_\mathcal{C}\to 0$ almost surely as $n\to\infty$ .

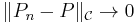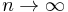2. $\|P_n-P\|_\mathcal{C}\to 0$ in probability as $n\to\infty$ .

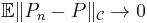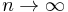3. $\mathbb{E}\|P_n-P\|_\mathcal{C}\to 0$ , as $n\to\infty$ (convergence in mean).

The Glivenko–Cantelli classes of functions are defined similarly.

A class is called a universal Glivenko–Cantelli class if it is a GC class with respect to any probability measure P on (S,A).
A class is called uniformly Glivenko–Cantelli if the convergence occurs uniformly over all probability measures P on (S,A):

$\sup_{P\in \mathcal{P}(S,A)} \mathbb E \|P_n-P\|_\mathcal{C}\to 0;$

$\sup_{P\in \mathcal{P}(S,A)} \mathbb E \|P_n-P\|_\mathcal{F}\to 0.$

Theorem (Vapnik and Chervonenkis,^[6] 1968)

A class of sets 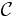$\mathcal{C}$ is uniformly GC if and only if it is a Vapnik–Chervonenkis class.

Examples

Let 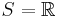$S=\mathbb R$ and ${\mathcal C}=\{(-\infty,t]:t\in {\mathbb R}\}$ . The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theorem,

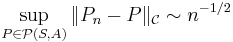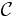$\sup_{P\in \mathcal{P}(S,A)}\|P_n-P\|_{\mathcal C} \sim n^{-1/2}$ , that is $\mathcal{C}$ is uniformly Glivenko–Cantelli class.

Let P be a nonatomic probability measure on S and 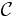$\mathcal{C}$ be a class of all finite subsets in S. Because 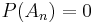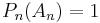$A_n=\{X_1,\ldots,X_n\}\in \mathcal{C}$ , $P(A_n)=0$ , $P_n(A_n)=1$ , we have that 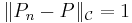$\|P_n-P\|_{\mathcal C}=1$ and so 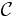$\mathcal{C}$ is not a GC class with respect to P.

Notes

^ van der Vaart, A.W. (1998) page 279
^ van der Vaart, A.W. (1998) page 265
^ Glivenko, V. (1933). Sulla determinazione empirica della legge di probabilita. Giorn. Ist. Ital. Attuari 4, 92-99.
^ Cantelli, F. P. (1933). Sulla determinazione empirica delle leggi di probabilita. Giorn. Ist. Ital. Attuari 4, 221-424.
^ van der Vaart, A.W. (1998) page 268
^ Vapnik, V.N. and Chervonenkis, A. Ya (1971). On uniform convergence of the frequencies of events to their probabilities. Theor. Prob. Appl. 16, 264-280

References

van der Vaart, A.W. (1998) Asymptotic Statistics. Cambridge University Press. ISBN 0-521-78450-6

Glivenko–Cantelli theorem

Contents