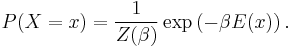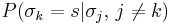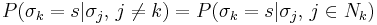Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble. Importantly, when the energy function can be written as a sum of parts, the Gibbs measure has the Markov property (a certain kind of statistical independence), thus leading to its widespread appearance in many problems outside of physics, such as Hopfield networks, Markov networks, and Markov logic networks. In addition, the Gibbs measure is the unique measure that maximizes the entropy for a given expected energy; thus, the Gibbs measure underlies maximum entropy methods and the algorithms derived therefrom.
The measure gives the probability of the system X being in state x (equivalently, of the random variable X having value x) as
Here, 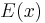 is a function from the space of states to the real numbers; in physics applications,
is a function from the space of states to the real numbers; in physics applications, 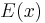 is interpreted as the energy of the configuration x. The parameter
is interpreted as the energy of the configuration x. The parameter  is a free parameter; in physics, it is the inverse temperature. The normalizing constant
is a free parameter; in physics, it is the inverse temperature. The normalizing constant 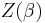 is the partition function.
is the partition function.
Contents |
Markov property
An example of the Markov property of the Gibbs measure can be seen in the Ising model. Here, the probability of a given spin 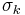 being in state s is, in principle, dependent on all other spins in the model; thus one writes
being in state s is, in principle, dependent on all other spins in the model; thus one writes
for this probability. However, the interactions in the Ising model are nearest-neighbor interactions, and thus, one actually has
where 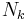 is the set of nearest neighbors of site
is the set of nearest neighbors of site  . That is, the probability at site
. That is, the probability at site  depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function;[1] this is the Hammersley–Clifford theorem.
depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function;[1] this is the Hammersley–Clifford theorem.
Gibbs measure on lattices
What follows is a formal definition for the special case of a random field on a group lattice. The idea of a Gibbs measure is, however, much more general than this.
The definition of a Gibbs random field on a lattice requires some terminology:
- The lattice: A countable set
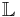 .
.
- The single-spin space: A probability space
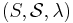 .
.
- The configuration space:
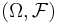 , where
, where 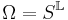 and
and 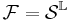 .
.
- Given a configuration
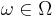 and a subset
and a subset 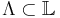 , the restriction of
, the restriction of  to
to 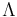 is
is 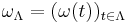 . If
. If 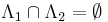 and
and 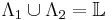 , then the configuration
, then the configuration 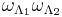 is the configuration whose restrictions to
is the configuration whose restrictions to 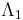 and
and 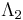 are
are 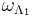 and
and 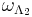 , respectively. These will be used to define cylinder sets, below.
, respectively. These will be used to define cylinder sets, below.
- The set
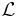 of all finite subsets of
of all finite subsets of 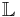 .
.
- For each subset
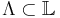 ,
, 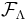 is the
is the  -algebra generated by the family of functions
-algebra generated by the family of functions 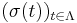 , where
, where 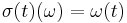 . This sigma-algebra is just the algebra of cylinder sets on the lattice.
. This sigma-algebra is just the algebra of cylinder sets on the lattice.
- The potential: A family
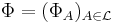 of functions
of functions 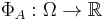 such that
such that
- For each
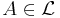 ,
, 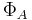 is
is 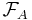 -measurable.
-measurable. - For all
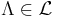 and
and 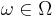 , the series
, the series 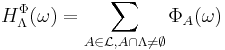 exists.
exists.
- For each
- The Hamiltonian in
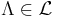 with boundary conditions
with boundary conditions 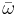 , for the potential
, for the potential 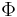 , is defined by
, is defined by
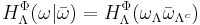 ,
,- where
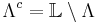 .
.
- The partition function in
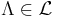 with boundary conditions
with boundary conditions 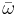 and inverse temperature
and inverse temperature 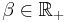 (for the potential
(for the potential 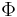 and
and  ) is defined by
) is defined by
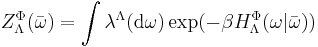 .
.- A potential
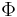 is
is  -admissible if
-admissible if 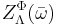 is finite for all
is finite for all 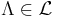 ,
, 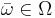 and
and 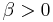 .
.
A probability measure  on
on 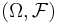 is a Gibbs measure for a
is a Gibbs measure for a  -admissible potential
-admissible potential 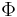 if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations
if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations
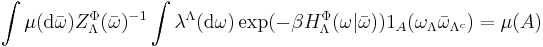 ,
,- for all
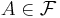 and
and 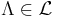 .
.
An example
To help understand the above definitions, here are the corresponding quantities in the important example of the Ising model with nearest-neighbour interactions (coupling constant 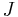 ) and a magnetic field (
) and a magnetic field ( ), on
), on 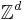 :
:
- The lattice is simply
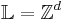 .
. - The single-spin space is
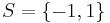 .
. - The potential is given by
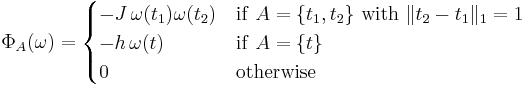
See also
References
- ^ Ross Kindermann and J. Laurie Snell, Markov Random Fields and Their Applications (1980) American Mathematical Society, ISBN 0-8218-5001-6
- Georgii, H.-O. "Gibbs measures and phase transitions", de Gruyter, Berlin, 1988.