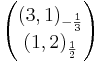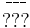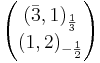Georgi–Glashow model
In particle physics, the Georgi–Glashow model is a particular grand unification theory (GUT) proposed by Howard Georgi and Sheldon Glashow in 1974. In this model the standard model gauge groups SU(3)×SU(2)×U(1) are combined into a single simple gauge group -- SU(5). The unified group SU(5) is then thought to be spontaneously broken to the standard model subgroup at some high energy scale called the grand unification scale.
Since the Georgi–Glashow model combines leptons and quarks into single irreducible representations, there exist interactions which do not conserve baryon number, although they still conserve B-L. This yields a mechanism for proton decay, and the rate of proton decay can be predicted from the dynamics of the model. However, proton decay has not yet been observed experimentally, and the resulting lower limit on the lifetime of the proton contradicts the predictions of this model. However, the elegance of the model has led particle physicists to use it as the foundation for more complex models which yield longer proton lifetimes.
(For a more elementary introduction to how the representation theory of Lie algebras are related to particle physics, see the article Particle physics and representation theory.)
This model suffers from the doublet-triplet splitting problem.
Contents |
Breaking SU(5)
SU(5) breaking occurs when a scalar field, analogous to the Higgs field, and transforming in the adjoint of SU(5) acquires a vacuum expectation value proportional to the weak hypercharge generator
When this occurs SU(5) is spontaneously broken to the subgroup of SU(5) commuting with the group generated by Y. This unbroken subgroup is just the standard model group: [SU(3)×SU(2)×U(1)_Y]/Z6.
Under the unbroken subgroup the adjoint 24 transforms as
giving the gauge bosons of the standard model. See restricted representation.
The standard model quarks and leptons fit neatly into representations of SU(5). Specifically, the left-handed fermions combine into 3 generations of 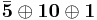 . Under the unbroken subgroup these transform as
. Under the unbroken subgroup these transform as
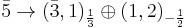 (dc and l)
(dc and l)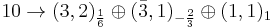 (q, uc and ec)
(q, uc and ec)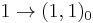 (νc)
(νc)
giving precisely the left-handed fermionic content of the standard model, where for every generation dc, uc, ec and νc stand for anti-down-type quark, anti-up-type quark, anti-down-type lepton and anti-up-type lepton, respectively, and q and l stand for quark and lepton. Note that fermions transforming as a 1 under SU(5) are now thought to be necessary because of the evidence for neutrino oscillations. Actually though, it is possible for there to be only left-handed neutrinos without any right-handed neutrinos if we could somehow introduce a tiny Majorana coupling for the left-handed neutrinos.
Since the homotopy group
this model predicts 't Hooft-Polyakov monopoles.
These monopoles have quantized Y magnetic charges. Since the electromagnetic charge Q is a linear combination of some SU(2) generator with Y/2, these monopoles also have quantized magnetic charges, where by magnetic here, we mean electromagnetic magnetic charges.
Minimal supersymmetric SU(5)
Spacetime
The N=1 superspace extension of 3+1 Minkowski spacetime.
Spatial symmetry
N=1 SUSY over 3+1 Minkowski spacetime without R-symmetry.
Gauge symmetry group
SU(5)
Global internal symmetry
Z2 (matter parity)
Matter parity
To prevent unwanted couplings in the supersymmetric version of the model, we assign a Z2 matter parity to the chiral superfields with the matter fields having odd parity and the Higgs having even parity. This is unnecessary in the nonsupersymmetric version, but then, we can't protect the electroweak Higgs from quadratic radiative mass corrections. See hierarchy problem. In the nonsupersymmetric version the action is invariant under a similar Z2 symmetry because the matter fields are all fermionic and thus must appear in the action in pairs, while the Higgs fields are bosonic.
Vector superfields
Those associated with the SU(5) gauge symmetry
Chiral superfields
As complex representations:
| label | description | multiplicity | SU(5) rep | 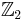 rep rep |
| Φ | GUT Higgs field | 1 | 24 | + |
| Hu | electroweak Higgs field | 1 | 5 | + |
| Hd | electroweak Higgs field | 1 | 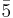 |
+ |
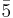 |
matter fields | 3 | 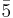 |
- |
| 10 | matter fields | 3 | 10 | - |
| Nc | sterile neutrinos | ??? | 1 | - |
Superpotential
A generic invariant renormalizable superpotential is a (complex) 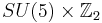 invariant cubic polynomial in the superfields. It is a linear combination of the following terms:
invariant cubic polynomial in the superfields. It is a linear combination of the following terms: 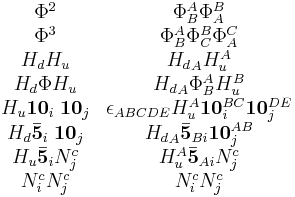
The first column is an Abbreviation of the second column (neglecting proper normalization factors), where capital indices are SU(5) indices, and i and j are the generation indices.
The last two rows presupposes the multiplicity of Nc is not zero (i.e. that a sterile neutrino exists). The coupling Hu 10i 10j has coefficients which are symmetric in i and j. The coupling NciNcj has coefficients which are symmetric in i and j. Note that the number of sterile neutrino generations need not be three, unless the SU(5) is embedded in a higher unification scheme such as SO(10).
Vacua
The vacua correspond to the mutual zeros of the F and D terms. Let's first look at the case where the VEVs of all the chiral fields are zero except for Φ.
The Φ sector
![W=Tr[a\Phi^2%2Bb\Phi^3]](/2012-wikipedia_en_all_nopic_01_2012/I/9590838711a20b558ada438974027b32.png)
The F zeros corresponds to finding the stationary points of W subject to the traceless constraint ![Tr[\Phi]=0](/2012-wikipedia_en_all_nopic_01_2012/I/fb63e7b4f70603db4193d2e3a3848eac.png) . So,
. So, 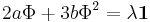 where λ is a Lagrange multiplier.
where λ is a Lagrange multiplier.
Up to an SU(5) (unitary) transformation,
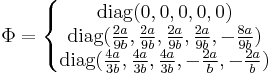
The three cases are called case I, II and III and they break the gauge symmetry into SU(5), ![[SU(4)\times U(1)]/\mathbb{Z}_4](/2012-wikipedia_en_all_nopic_01_2012/I/7a8e911bdbb2c5d52fe96708a5bcffb8.png) and
and ![[SU(3)\times SU(2)\times U(1)]/\mathbb{Z}_6](/2012-wikipedia_en_all_nopic_01_2012/I/dfa646763d4e7690af5ca231084a3ab9.png) respectively (the stabilizer of the VEV).
respectively (the stabilizer of the VEV).
In other words, there at least three different superselection sections, which is typical for supersymmetric theories.
Only case III makes any phenomenological sense and so, we will focus on this case from now onwards.
It can be verified that this solution together with zero VEVs for all the other chiral multiplets is a zero of the F-terms and D-terms. The matter parity remains unbroken (right up to the TeV scale).
Decomposition
The gauge algebra 24 decomposes as 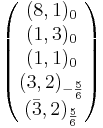 . This 24 is a real representation, so the last two terms need explanation. Both
. This 24 is a real representation, so the last two terms need explanation. Both 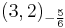 and
and 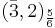 are complex representations. However, the direct sum of both representation decomposes into two irreducible real representations and we only take half of the direct sum, i.e. one of the two real irreducible copies. The first three components are left unbroken. The adjoint Higgs also has a similar decomposition, except that it is complex. The Higgs mechanism causes one real HALF of the
are complex representations. However, the direct sum of both representation decomposes into two irreducible real representations and we only take half of the direct sum, i.e. one of the two real irreducible copies. The first three components are left unbroken. The adjoint Higgs also has a similar decomposition, except that it is complex. The Higgs mechanism causes one real HALF of the 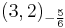 and
and 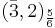 of the adjoint Higgs to be absorbed. The other real half acquires a mass coming from the D-terms. And the other three components of the adjoint Higgs,
of the adjoint Higgs to be absorbed. The other real half acquires a mass coming from the D-terms. And the other three components of the adjoint Higgs, 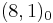 ,
, 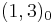 and
and 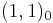 acquire GUT scale masses coming from self pairings of the superpotential, aΦ2+b<Φ>Φ2.
acquire GUT scale masses coming from self pairings of the superpotential, aΦ2+b<Φ>Φ2.
The sterile neutrinos, if any exists, would also acquire a GUT scale Majorana mass coming from the superpotential coupling νc2.
Because of matter parity, the matter representations 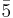 and 10 remain chiral.
and 10 remain chiral.
It's the Higgs fields 5H and 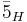 which are interesting.
which are interesting.
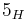 |
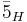 |
|
|
|
|
|
The two relevant superpotential terms here are 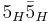 and
and 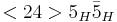 . Unless there happens to be some fine tuning, we would expect both the triplet terms and the doublet terms to pair up, leaving us with no light electroweak doublets. This is in complete disagreement with phenomenology. See doublet-triplet splitting problem for more details.
. Unless there happens to be some fine tuning, we would expect both the triplet terms and the doublet terms to pair up, leaving us with no light electroweak doublets. This is in complete disagreement with phenomenology. See doublet-triplet splitting problem for more details.
Fermion masses
See Georgi-Jarlskog mass relation.
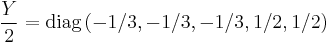
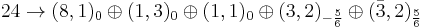
![\pi_2\left(\frac{SU(5)}{[SU(3)\times SU(2)\times U(1)_Y]/\mathbb{Z}_6}\right)=\mathbb{Z}](/2012-wikipedia_en_all_nopic_01_2012/I/5869c7d877c93b42e1ad1e3b0a71203f.png)