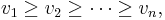Generalized second-price auction
The generalized second-price auction (GSP) is a non-truthful auction mechanism for multiple items. First thought of as a natural extension of the Vickrey auction, it actually doesn't conserve some good properties of the Vickrey auction (as truthfulness, for example). It is used mainly in the context of keyword auctions, where sponsored search slots are sold on an auction-base. The first analysis of GSP are in the economics literature by Edelman, Ostrovsky and Schwarz[1] and by Varian. [2] It is employed by Google's AdWords technology.
Contents |
Formal model
Consider there are  bidders and
bidders and 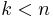 slots. Each slot has a probability of being clicked of
slots. Each slot has a probability of being clicked of 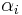 . We can assume that top slots have a larger probability of being clicked, so:
. We can assume that top slots have a larger probability of being clicked, so:
We can think of 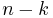 additional virtual slots with click-through-rate zero, so,
additional virtual slots with click-through-rate zero, so, 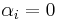 for
for  . Now, each bidder has an intrinsic value for one slot
. Now, each bidder has an intrinsic value for one slot 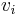 submits a bid
submits a bid 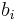 indicating the maximum he is willing to pay for a slot (which is his bid reported valuation - notice it doesn't need to be the same as his true valuation
indicating the maximum he is willing to pay for a slot (which is his bid reported valuation - notice it doesn't need to be the same as his true valuation 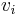 ). We order the bidders by their value, let's say:
). We order the bidders by their value, let's say:
and charge each bidder a price 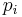 (this will be 0 if they didn't win a slot). Slots are sold in a pay-per-click model, so a bidder just pays for a slot if the user actually clicks in that slot. We say the utility of bidder
(this will be 0 if they didn't win a slot). Slots are sold in a pay-per-click model, so a bidder just pays for a slot if the user actually clicks in that slot. We say the utility of bidder  when allocated to slot
when allocated to slot  is
is 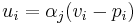 . The total social welfare from owning or selling slots is given by:
. The total social welfare from owning or selling slots is given by: 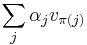 where
where 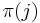 is the bidder allocated to slot
is the bidder allocated to slot  . The total revenue is given by:
. The total revenue is given by: 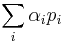
GSP mechanism
To specify a mechanism we need to define the allocation rule (who gets which slot) and the prices paid by each bidder. In GSP we order the bidders by their bid and give the top slot to the highest bidder, the second top slot to the second highest bidder and so on... So, bidder  gets slot
gets slot  . Each bidder pays the bid of the next highest bidder, so:
. Each bidder pays the bid of the next highest bidder, so: 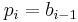 ..
..
Non-truthfulness
There are cases where bidding the true valuation is not a Nash equilibrium. For example, consider two slots with 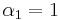 and
and 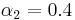 and three bidders with valuations
and three bidders with valuations 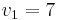 ,
, 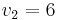 and
and 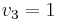 . Bidding 7, 6 and 1 respectively is not a Nash equilibrium, since the first bidder could lower his bid to 5 and get the second slot for the price of 1 and increase his utility therefore.
. Bidding 7, 6 and 1 respectively is not a Nash equilibrium, since the first bidder could lower his bid to 5 and get the second slot for the price of 1 and increase his utility therefore.
Equilibria of GSP
Edelman, Ostrovsky and Schwarz [1] show that GSP (in the model presented above) has always an efficient equilibrium, i.e., an equilibrium maximizing social welfare, which is measured as 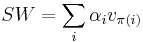 where
where 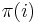 is the slot in which player
is the slot in which player  is allocated according to his bid (the permutation
is allocated according to his bid (the permutation  is defined by the bid vector
is defined by the bid vector  ). This equilibrium has the property that the outcome (allocation and payments) is the similar of VCG. The same papers study properties of a natural but restricted class of equilibria called envy-free equilibria. They prove that envy-free equilibria always exist and it always maximizes the social welfare - they also compare the revenue on different envy-free equilibria. Lahaie [3] studies the GSP from a Theoretical Computer Science point of view. Paes Leme and Tardos [4] study the structure of the general equilibria in GSP and prove Price of Anarchy. They prove that the Price of Anarchy under a set of natural conditions is bounded by
). This equilibrium has the property that the outcome (allocation and payments) is the similar of VCG. The same papers study properties of a natural but restricted class of equilibria called envy-free equilibria. They prove that envy-free equilibria always exist and it always maximizes the social welfare - they also compare the revenue on different envy-free equilibria. Lahaie [3] studies the GSP from a Theoretical Computer Science point of view. Paes Leme and Tardos [4] study the structure of the general equilibria in GSP and prove Price of Anarchy. They prove that the Price of Anarchy under a set of natural conditions is bounded by 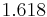 (golden ratio). Computational analysis of this game have been performed by Thompson and Leyton-Brown.[5]
(golden ratio). Computational analysis of this game have been performed by Thompson and Leyton-Brown.[5]
GSP and uncertainty
The classical results due to Edelman, Ostrovsky and Schwarz [1] and Varian [2] hold in the full information setting - when there is no uncertainty involved. Recent results as Gomes and Sweeney [6] and Paes Leme and Tardos [4] and also empirically by Athey and Nikipelov [7] discuss the Bayesian version of the game - where players have beliefs about the other players, but not necessarily know the other players valuations. Gomes and Sweeney [6] prove that an efficient equilibrium might not exist in the partial information setting. Paes Leme and Tardos [4] prove a bound of 8 for the Bayes-Nash Price of Anarchy.
See also
References
- ^ a b c Benjamin Edelman, Michael Ostrovsky, and Michael Schwarz: "Internet Advertising and the Generalized Second-Price Auction: Selling Billions of Dollars Worth of Keywords". American Economic Review 97(1), 2007 pp 242-259
- ^ a b H. R. Varian. Position auctions. International Journal of Industrial Organization, 2006.
- ^ S. Lahaie. An analysis of alternative slot auction designs for sponsored search. In EC ’06: Proceedings of the 7th ACMconference on Electronic commerce, pages 218–227
- ^ a b c Renato Paes Leme and Eva Tardos, Pure and Bayes-Nash Price of Anarchy for Generalized Second Price Auction, 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS 2010)
- ^ D. R. M. Thompson and K. Leyton-Brown. Computational analysis of perfect-information position auctions. In EC ’09: Proceedings of the tenth ACM conference on Electronic commerce, pages 51–60, New York, NY, USA, 2009. ACM.
- ^ a b R. D. Gomes and K. S. Sweeney. Bayes-nash equilibria of the generalized second price auction. In EC ’09: Proceedings of the tenth ACM conference on Electronic commerce, pages 107–108, New York, NY, USA, 2009. ACM
- ^ Susan Athey and Denis Nekipelov. A Structural Model of Sponsored Search Advertising Auctions, Ad Auctions Workshop, 2010
- S. Lahaie, D. Pennock, A. Saberi, and R. Vohra. Algorithmic Game Theory, chapter "Sponsored search auctions:, pages 699–716. Cambridge University Press,
2007
- Lecture notes on Keyword-Based Advertisement