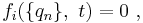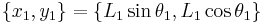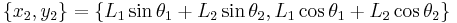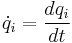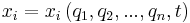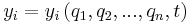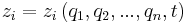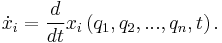Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration. A restriction for a set of coordinates to serve as generalized coordinates is that they should uniquely define any possible configuration of the system relative to the reference configuration.[1] Frequently the generalized coordinates are chosen to be independent of one another. The number of independent generalized coordinates is defined by the number of degrees of freedom of the system.[2] The adjective "generalized" is a holdover from a period when Cartesian coordinates were the standard.
Apart from practical reasons, any set of generalized coordinates is as good as another. The physics of the system is independent of the choice. However, there are more and less practical choices, that is, coordinates that are more or less optimally adapted to the system and make the solution of its equations of motion easier or more difficult.[3]
The generalized velocities are the time derivatives of the generalized coordinates of the system.
Contents |
Constraint equations
Generalized coordinates may be independent (or unconstrained), in which case they are equal in number to the degrees of freedom of the system, or they may be dependent (or constrained), related by constraints on and among the coordinates. The number of dependent coordinates is the sum of the number of degrees of freedom and the number of constraints. For example, the constraints might take the form of a set of configuration constraint equations:[1]
where qn is the n-th generalized coordinate and i denotes one of a set of constraint equations, taken here to vary with time t. The constraint equations limit the values available to the set of qn, and thereby exclude certain configurations of the system.
It can be advantageous to choose independent generalized coordinates, as is done in Lagrangian mechanics, because this eliminates the need for constraint equations. However, in some situations, it is not possible to identify an unconstrained set. For example, when dealing with nonholonomic constraints or when trying to find the force due to any constraint—holonomic or not, dependent generalized coordinates must be employed. Sometimes independent generalized coordinates are called internal coordinates because they are mutually independent, otherwise unconstrained, and together give the position of the system.
A system with  degrees of freedom and n particles whose positions are designated with three dimensional vectors,
degrees of freedom and n particles whose positions are designated with three dimensional vectors, 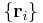 , implies the existence of
, implies the existence of 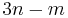 scalar constraint equations on those position variables. Such a system can be fully described by the scalar generalized coordinates,
scalar constraint equations on those position variables. Such a system can be fully described by the scalar generalized coordinates,  , and the time,
, and the time,  , if and only if all
, if and only if all 
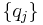 are independent coordinates. For the system, the transformation from old coordinates to generalized coordinates may be represented as follows:[4]:260
are independent coordinates. For the system, the transformation from old coordinates to generalized coordinates may be represented as follows:[4]:260
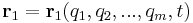 ,
,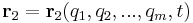 , ...
, ...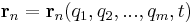 .
.
This transformation affords the flexibility in dealing with complex systems to use the most convenient and not necessarily inertial coordinates. These equations are used to construct differentials when considering virtual displacements and generalized forces.
Examples
Double pendulum
A double pendulum constrained to move in a plane may be described by the four Cartesian coordinates {x1, y1, x2, y2}, but the system only has two degrees of freedom, and a more efficient system would be to use
 ,
,
which are defined via the following relations:
Bead on a wire
A bead constrained to move on a wire has only one degree of freedom, and the generalized coordinate used to describe its motion is often
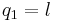 ,
,
where l is the distance along the wire from some reference point on the wire. Notice that a motion embedded in three dimensions has been reduced to only one dimension.
Motion on a surface
A point mass constrained to a surface has two degrees of freedom, even though its motion is embedded in three dimensions. If the surface is a sphere, a good choice of coordinates would be:
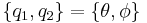 ,
,
where θ and φ are the angle coordinates familiar from spherical coordinates. The r coordinate has been effectively dropped, as a particle moving on a sphere maintains a constant radius.
Generalized velocities and kinetic energy
Each generalized coordinate 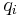 is associated with a generalized velocity
is associated with a generalized velocity 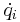 , defined as:
, defined as:
The kinetic energy of a particle is
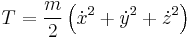 .
.
In more general terms, for a system of  particles with
particles with  degrees of freedom, this may be written
degrees of freedom, this may be written
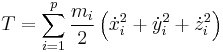 .
.
If the transformation equations between the Cartesian and generalized coordinates
are known, then these equations may be differentiated to provide the time-derivatives to use in the above kinetic energy equation:
It is important to remember that the kinetic energy must be measured relative to inertial coordinates. If the above method is used, it means only that the Cartesian coordinates need to be inertial, even though the generalized coordinates need not be. This is another considerable convenience of the use of generalized coordinates.
Applications of generalized coordinates
Such coordinates are helpful principally in Lagrangian mechanics, where the forms of the principal equations describing the motion of the system are unchanged by a shift to generalized coordinates from any other coordinate system. The amount of virtual work done along any coordinate 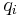 is given by:
is given by:
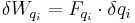 ,
,
where 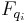 is the generalized force in the
is the generalized force in the 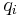 direction. While the generalized force is difficult to construct 'a priori', it may be quickly derived by determining the amount of work that would be done by all non-constraint forces if the system underwent a virtual displacement of
direction. While the generalized force is difficult to construct 'a priori', it may be quickly derived by determining the amount of work that would be done by all non-constraint forces if the system underwent a virtual displacement of 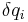 , with all other generalized coordinates and time held fixed. This will take the form:
, with all other generalized coordinates and time held fixed. This will take the form:
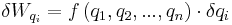 ,
,
and the generalized force may then be calculated:
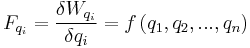 .
.
See also
- Hamiltonian mechanics
- Virtual work
- Orthogonal coordinates
- Curvilinear coordinates
- Frenet-Serret formulas
- Mass matrix
- Stiffness matrix
References
- ^ a b Jerry H. Ginsberg (2008). "§7.2.1 Selection of generalized coordinates". Engineering dynamics, Volume 10 (3rd ed.). Cambridge University Press. p. 397. ISBN 0521883032. http://books.google.com/books?id=je0W8N5oXd4C&pg=PA397.
- ^ Farid M. L. Amirouche (2006). "§2.4: Generalized coordinates". Fundamentals of multibody dynamics: theory and applications. Springer. p. 46. ISBN 0817642366. http://books.google.com/books?id=_nlEcQYldeIC&pg=PA46.
- ^ Florian Scheck (2010). "§5.1 Manifolds of generalized coordinates". Mechanics: From Newton's Laws to Deterministic Chaos (5th ed.). Springer. p. 286. ISBN 3642053696. http://books.google.com/books?id=yUDo7VptDgIC&pg=PA286.
- ^ Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
- Greenwood, Donald T. (1987). Principles of Dynamics (2nd edition ed.). Prentice Hall. ISBN 0-13-709981-9.
- Wells, D. A. (1967). Schaum's Outline of Lagrangian Dynamics. New York: McGraw-Hill.