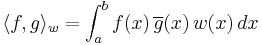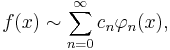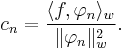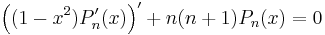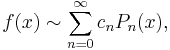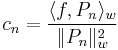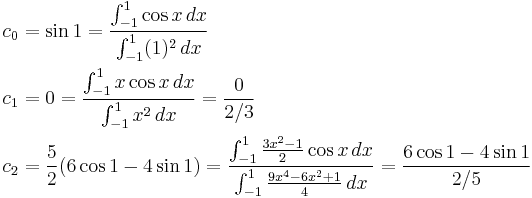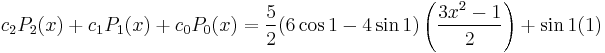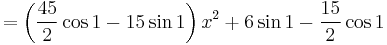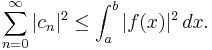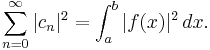Generalized Fourier series

In mathematical analysis, many generalizations of Fourier series have proved to be useful. They are all special cases of decompositions over an orthonormal basis of an inner product space. Here we consider that of square-integrable functions defined on an interval of the real line, which is important, among others, for interpolation theory.

Contents

Definition

Consider a set of square-integrable functions with values in 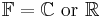\mathbb{F}=\mathbb{C}\mbox{ or }\mathbb{R},

\Phi = \{\varphi_n:[a,b]\rightarrow \mathbb{F}\}_{n=0}^\infty,

which are pairwise orthogonal for the inner product

\langle f, g\rangle_w = \int_a^b f(x)\,\overline{g}(x)\,w(x)\,dx

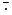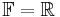where w(x) is a weight function, and \overline\cdot represents complex conjugation, i.e. \overline{g}(x)=g(x) for \mathbb{F}=\mathbb{R}.

The generalized Fourier series of a square-integrable function f: [a, b] → 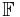\mathbb{F}, with respect to Φ, is then

f(x) \sim \sum_{n=0}^\infty c_n\varphi_n(x),

where the coefficients are given by

c_n = {\langle f, \varphi_n \rangle_w\over \|\varphi_n\|_w^2}.

If Φ is a complete set, i.e., an orthonormal basis of the space of all square-integrable functions on [a, b], as opposed to a smaller orthonormal set, the relation 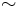\sim \, becomes equality in the L² sense, more precisely modulo |·|w (not necessarily pointwise, nor almost everywhere).

Example (Fourier–Legendre series)

The Legendre polynomials are solutions to the Sturm–Liouville problem

\left((1-x^2)P_n'(x)\right)'%2Bn(n%2B1)P_n(x)=0

and because of the theory, these polynomials are eigenfunctions of the problem and are solutions orthogonal with respect to the inner product above with unit weight. So we can form a generalized Fourier series (known as a Fourier–Legendre series) involving the Legendre polynomials, and

f(x) \sim \sum_{n=0}^\infty c_n P_n(x),
c_n = {\langle f, P_n \rangle_w\over \|P_n\|_w^2}

As an example, let us calculate the Fourier–Legendre series for ƒ(x) = cos x over [−1, 1]. Now,

\begin{align} c_0 & = \sin{1} = {\int_{-1}^1 \cos{x}\,dx \over \int_{-1}^1 (1)^2 \,dx} \\ c_1 & = 0 = {\int_{-1}^1 x \cos{x}\,dx \over \int_{-1}^1 x^2 \, dx} = {0 \over 2/3 } \\ c_2 & = {5 \over 2} (6 \cos{1} - 4\sin{1}) = {\int_{-1}^1 {3x^2 - 1 \over 2} \cos{x} \, dx \over \int_{-1}^1 {9x^4-6x^2%2B1 \over 4} \, dx} = {6 \cos{1} - 4\sin{1} \over 2/5 } \end{align}

and a series involving these terms

c_2P_2(x)%2Bc_1P_1(x)%2Bc_0P_0(x)= {5 \over 2} (6 \cos{1} - 4\sin{1})\left({3x^2 - 1 \over 2}\right) %2B \sin{1}(1)
= \left({45 \over 2} \cos{1} - 15 \sin{1}\right)x^2%2B6 \sin{1} - {15 \over 2}\cos{1}

which differs from cos x by approximately 0.003, about 0. It may be advantageous to use such Fourier–Legendre series since the eigenfunctions are all polynomials and hence the integrals and thus the coefficients are easier to calculate.

Coefficient theorems

Some theorems on the coefficients cn include:

Bessel's inequality

\sum_{n=0}^\infty |c_n|^2\leq\int_a^b|f(x)|^2\,dx.

Parseval's theorem

If Φ is a complete set,

\sum_{n=0}^\infty |c_n|^2 = \int_a^b|f(x)|^2\, dx.

See also