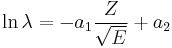Geiger–Nuttall law
In nuclear physics, the Geiger–Nuttall law or Geiger–Nuttall rule relates the decay constant of a radioactive isotope with the energy of the alpha particles emitted. Roughly speaking, it states that short-lived isotopes emit more energetic alpha particles than long-lived ones.
The relationship also shows that half-lives are exponentially dependent on decay energy, so that very large changes in half-life make comparatively small differences in decay energy, and thus alpha particle energy. In practice, this means that alpha particles from all alpha-emitting isotopes across many orders of magnitude of difference in half-life, all nevertheless have about the same decay energy.
Formulated in 1911 by Hans Geiger and John Mitchell Nuttall,[1] in its modern form the Geiger–Nuttall law is
where λ is the decay constant (λ = ln2/half-life), Z the atomic number, E the total kinetic energy (of the alpha particle and the daughter nucleus), and a1 and a2 are constants.
Derivation
A simple way to derive this law is to consider an alpha particle in the atomic nucleus as a particle in a box. The particle is in a bound state because of the presence of the strong interaction potential. It will constantly bounce from one side to the other, and due to the possibility of quantum tunneling by the wave though the potential barrier, each time it bounces, there will be a small likelihood for it to escape.
A knowledge of this quantum mechanical effect enables one to obtain this law, including coefficients, via direct calculation.[1] This calculation was first performed by physicist George Gamow in 1928.[2]
References
- ^ H. Geiger and J.M. Nuttall (1911) "The ranges of the α particles from various radioactive substances and a relation between range and period of transformation," Philosophical Magazine, Series 6, vol. 22, no. 130, pages 613-621. See also: H. Geiger and J.M. Nuttall (1912) "The ranges of α particles from uranium," Philosophical Magazine, Series 6, vol. 23, no. 135, pages 439-445.
- ^ G. Gamow (1928) "Zur Quantentheorie des Atomkernes" (On the quantum theory of the atomic nucleus), Zeitschrift für Physik, vol. 51, pages 204-212.