Gas dynamics
Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics. This study often concentrates on the behaviour of gases flowing at speeds comparable to the speed of sound, making it relevant in the design of aircraft and spacecraft and their propulsion systems.
Contents |
Introduction
Gas dynamics is the overview of the average value in the distance between two molecules of gas that has collided with out ignoring the structure in which the molecules are contained. The field requires a great amount of knowledge and practical use in the ideas of the kinetic theory of gases, and it links the kinetic theory of gases with the solid state physics through the study of how gas reacts with surfaces[1].
Definition of a Fluid
Fluids are substances that do not permanently change under an enormous amount of stress. A solid tends to deform in order to remain at equilibrium under a great deal of stress. Fluids are defined as both liquids and gases because the molecules inside the fluid are much weaker than those molecules contained in a solid. When referring to the density of a fluid in terms of a liquid, there is a small percentage of change to the liquid’s density as pressure is increased. If the fluid is referred to as a gas, the density will change greatly depending on the amount of pressure applied due to the equation of state for gases (p=ρRT). In the study of the flow of liquids, the term used while referring to the little change in density is called incompressible flow. In the study of the flow of gases, the rapid increase due to an increase of pressure is called compressible flow[2].
Real Gases
Real gases are commonly referred to as ideal gases. Real gases are characterized by their compressibility (z) in the equation PV=z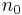 RT. When the pressure, P, is set as a function of the volume, V, where the series is determined by set temperatures, T, P and V began to take hyperbolic relationships that are exhibited by ideal gases as the temperatures start to get very high. A critical point is reached when the slope of the graph is equal to zero and makes the state of the fluid change between a liquid and a vapor. The properties of ideal gases contain viscosity, thermal conductivity, and diffusion[3].
RT. When the pressure, P, is set as a function of the volume, V, where the series is determined by set temperatures, T, P and V began to take hyperbolic relationships that are exhibited by ideal gases as the temperatures start to get very high. A critical point is reached when the slope of the graph is equal to zero and makes the state of the fluid change between a liquid and a vapor. The properties of ideal gases contain viscosity, thermal conductivity, and diffusion[3].
Viscosity
The viscosity of gases is the result in the transfer of each molecule of gas as they pass each other from layer to layer. As gases tend to pass one another, the velocity, in the form of momentum, of the faster moving molecule speeds up the slower moving molecule. As the slower moving molecule passes the faster moving molecule, the momentum of the slower moving particle slows down the faster moving particle. The molecules continue to enact until frictional drag causes both molecules to equalize their velocities[4].
Thermal Conductivity
The thermal conductivity of a gas can be found through analysis of a gas’ viscosity except the molecules are stationary while only the temperatures of the gases are changing. Thermal conductivity is stated as the amount of heat transported across a specific area in a specific time. The thermal conductivity always flows opposite of the direction of the temperature gradient[5].
Diffusion
Diffusion of gases is configured with a uniform concentration of gases and while the gases are stationary. Diffusion is the change of concentration between the two gases due to a weaker concentration gradient between the two gases. Diffusion is the transportation of mass over a period of time[6].
Shock Waves
A shock wave is a compressional force that is created by an abrupt change in fluid properties such as pressure, temperature, and density. Shockwaves can be established in two types of flows: subsonic and supersonic. The subsonic flow is adjusted by changes in the flow properties while the supersonic flow is the adjusted through the change of the presence of an object[7].
Stationary Normal Shock Waves
A stationary normal shock wave is classified as going in the normal direction of the flow direction. For example, when a piston moves at a constant rate inside a tube, sound waves that travel down the tube are produced. As the piston continues to move, the wave begins to come together and compresses the gas inside the tube. The various calculations that come along side of normal shock waves can vary due to the size of the tubes in which they are contained. Abnormalities such as converging-diverging nozzles and tubes with changing areas can affect such calculations as volume, pressure, and Mach number.[8].
Moving Normal Shock Waves
Unlike stationary normal shockwaves, moving normal shockwaves are more commonly available in physical situations. For example, a blunt object entering into the atmosphere faces a shock that comes through the medium of a non-moving gas. The fundamental problem that comes through moving normal shockwaves is the moment of a normal shockwave through motionless gas. The viewpoint of the moving shockwaves characterizes it as a moving or non-moving shock wave. The example of an object entering into the atmosphere depicts an object traveling in the opposite direction of the shockwave resulting in a moving shockwave, but if the object was launching into space, riding on top of the shockwave, it would appear to be a stationary shockwave. The relations and comparisons along with speed and shock ratios of moving and stationary shockwaves can be calculated through extensive formulas[9].
Friction and Compressible Flow
Frictional forces play a role in determining the flow properties of compressible flow in ducts. In calculations, friction is either taken as inclusive or exclusive. If friction is inclusive, then the analysis of compressible flow becomes more complex as if friction is not inclusive. If the friction is exclusive to the analysis, then certain restrictions will be put into place. When friction is included on compressible flow, the friction limits the areas in which the results from analysis in be applied. As mentioned before, the shape of the duct, such as varying sizes or nozzles, effect the different calculations in between friction and compressible flow [10].
References
- ^ Cercignani, Carlo. Preface. Rarefied Gas Dynamics: from Basic Concepts to Actual Calculations. Cambridge UP, 2000. Xiii. Print.
- ^ John, James Edward Albert., and Theo G. Keith. Gas Dynamics. Harlow: Prentice Hall, 2006. 1-2. Print
- ^ Turrell, George. Gas Dynamics: Theory and Applications. Chichester: J. Wiley, 1997. 45-53. Print
- ^ Turrell, George. Gas Dynamics: Theory and Applications. Chichester: J. Wiley, 1997. 31-33. Print
- ^ Turrell, George. Gas Dynamics: Theory and Applications. Chichester: J. Wiley, 1997. 33-34. Print
- ^ Turrell, George. Gas Dynamics: Theory and Applications. Chichester: J. Wiley, 1997. 34-35. Print
- ^ John, James Edward Albert., and Theo G. Keith. Gas Dynamics. 3rd ed. Harlow: Prentice Hall, 2006. 107. Print.
- ^ John, James Edward Albert., and Theo G. Keith. Gas Dynamics. 3rd ed. Harlow: Prentice Hall, 2006. 107-149. Print.
- ^ John, James Edward Albert., and Theo G. Keith. Gas Dynamics. 3rd ed. Harlow: Prentice Hall, 2006. 157-184. Print.
- ^ John, James Edward Albert., and Theo G. Keith. Gas Dynamics. 3rd ed. Harlow: Prentice Hall, 2006. 283-336. Print.
See also
|
Important concepts |
Flows of interest |
Experimental techniques |
|
Visualisation methods |
Computational techniques |
Aerodynamics |
References
- Liepmann, Hans W.; Roshko, A. (2001) [1957]. Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0.
- Anderson, John D. Jr. (January 2001) [1984]. Fundamentals of Aerodynamics (3rd Edition ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-237335-0.
- Shapiro, Ascher H.. The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0.
- Zucker, Robert D.; Biblarz O. (July 2002). Fundamentals of Gas Dynamics. John Wiley & Sons. ISBN 0471059676.
- Vincenti, Walter G.; Kruger, Charles H., Jr. (2002) [1965]. Introduction to Physical Gas Dynamics. Krieger publishing company. ISBN 0-88275-309-6.
- Anderson, John D. Jr. (2000) [1989]. hypersonic and High Temperature Gas Dynamics. AIAA. ISBN 1-56347-459-X.