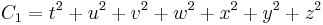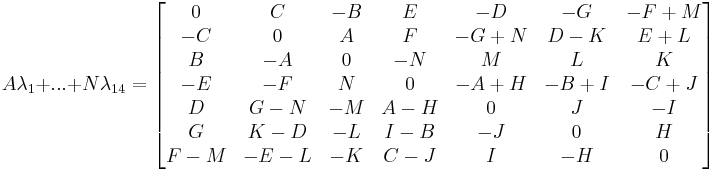G2 (mathematics)
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
| Lie groups |
|---|
|
General linear group GL(n)
Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) |
|
|
In mathematics, G2 is the name of three simple Lie groups (a complex form, a compact real form and a split real form), their Lie algebras 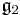 , as well as some algebraic groups. They are the smallest of the five exceptional simple Lie groups. G2 has rank 2 and dimension 14. Its fundamental representation is 7-dimensional.
, as well as some algebraic groups. They are the smallest of the five exceptional simple Lie groups. G2 has rank 2 and dimension 14. Its fundamental representation is 7-dimensional.
The compact form of G2 can be described as the automorphism group of the octonion algebra or, equivalently, as the subgroup of 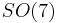 that preserves any chosen particular vector in its 8-dimensional real spinor representation.
that preserves any chosen particular vector in its 8-dimensional real spinor representation.
In older books and papers, G2 is sometimes denoted by E2.
Contents |
Real forms
There are 3 simple real Lie algebras associated with this root system:
- The underlying real Lie algebra of the complex Lie algebra G2 has dimension 28. It has complex conjugation as an outer automorphism and is simply connected. The maximal compact subgroup of its associated group is the compact form of G2.
- The Lie algebra of the compact form is 14 dimensional. The associated Lie group has no outer automorphisms, no center, and is simply connected and compact.
- The Lie algebra of the non-compact (split) form has dimension 14. The associated simple Lie group has fundamental group of order 2 and its outer automorphism group is the trivial group. Its maximal compact subgroup is SU(2)×SU(2)/(−1×−1). It has a non-algebraic double cover that is simply connected.
Algebra
Dynkin diagram and Cartan matrix
The Dynkin diagram for G2 is given by or
Its Cartan matrix is:
Roots of G2
The 12 vector root system of G2 in 2 dimensions. |
The A2 Coxeter plane projection of the 12 vertices of the cuboctahedron contain the same 2D vector arrangement. |
Graph of G2 as a subgroup of F4 and E8 projected into the Coxeter plane |
Although they span a 2-dimensional space, as drawn, it's much more symmetric to consider them as vectors in a 2-dimensional subspace of a three dimensional space.
|
|
Simple roots
- (0,1,−1), (1,−2,1)
Weyl/Coxeter group
Its Weyl/Coxeter group is the dihedral group, D6 of order 12.
Special holonomy
G2 is one of the possible special groups that can appear as the holonomy group of a Riemannian metric. The manifolds of G2 holonomy are also called G2-manifolds.
Polynomial Invariant
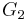 is the automorphism group of the following two polynomials in 7 non-commutative variables.
is the automorphism group of the following two polynomials in 7 non-commutative variables.
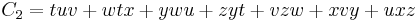 (± permutations)
(± permutations)
which comes from the octionion algebra. The variables must be non-commutative otherwise the second polynomial would be identically zero.
Generators
Adding a representation of the 14 generators with coefficients A..N gives the matrix:
Representations
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formula. The dimensions of the smallest irreducible representations are (sequence A104599 in OEIS):
- 1, 7, 14, 27, 64, 77 (twice), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (twice), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (twice), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090….
The 14-dimensional representation is the adjoint representation, and the 7-dimensional one is action of G2 on the imaginary octonions.
There are two non-isomorphic irreducible representations of dimensions 77, 2079, 4928, 28652, etc. The fundamental representations are those with dimensions 14 and 7 (corresponding to the two nodes in the Dynkin diagram in the order such that the triple arrow points from the first to the second).
Vogan (1994) described the (infinite dimensional) unitary irreducible representations of the.split real form of G2.
Finite groups
Leonard Eugene Dickson introduced the finite groups G2(Fq) in Dickson (1901) for odd q and Dickson (1905) for even q. The group G2(Fq) is the points of the algebraic group G2 over the finite field Fq. The order of the group is q6(q6−1)(q2−1). When q ≠ 2, the group is simple, and when q = 2, it has a simple subgroup of index 2 isomorphic to 2A2(32). The Janko group J1 was first constructed as a subgroup of G2(F11). Ree (1960) introduced twisted Ree groups 2G2(Fq) of order q3(q3+1)(q−1) for q=32n+1 an odd power of 3.
See also
References
- Adams, J. Frank (1996), Lectures on exceptional Lie groups, Chicago Lectures in Mathematics, University of Chicago Press, ISBN 978-0-226-00526-3, MR1428422, http://books.google.com/books?isbn=0226005275
- Agricola, Ilka (2008), Old and New on the Exceptional Group G2, 55, http://www.ams.org/notices/200808/tx080800922p.pdf
- Baez, John (2002), "The Octonions", Bull. Amer. Math. Soc. 39 (2): 145–205, doi:10.1090/S0273-0979-01-00934-X, http://www.ams.org/bull/2002-39-02/S0273-0979-01-00934-X/home.html.
-
- See section 4.1: G2; an online HTML version of which is available at http://math.ucr.edu/home/baez/octonions/node14.html.
- Dickson, Leonard Eugene (1901), "Theory of Linear Groups in An Arbitrary Field" (in English), Transactions of the American Mathematical Society (Providence, R.I.: American Mathematical Society) 2 (4): 363–394, doi:10.1090/S0002-9947-1901-1500573-3, ISSN 0002-9947, JSTOR 1986251, Reprinted in volume II of his collected papers Leonard E. Dickson reported groups of type G2 in fields of odd characteristic.
- Dickson, L. E. (1905), "A new system of simple groups", Math. Ann. 60: 137–150, doi:10.1007/BF01447497 Leonard E. Dickson reported groups of type G2 in fields of even characteristic.
- Ree, Rimhak (1960), "A family of simple groups associated with the simple Lie algebra of type (G2)", Bulletin of the American Mathematical Society 66 (6): 508–510, doi:10.1090/S0002-9904-1960-10523-X, ISSN 0002-9904, MR0125155, http://www.ams.org/journals/bull/1960-66-06/S0002-9904-1960-10523-X/home.html
- Vogan, David A. Jr. (1994), "The unitary dual of G2", Inventiones Mathematicae 116 (1): 677–791, doi:10.1007/BF01231578, ISSN 0020-9910, MR1253210, http://dx.doi.org/10.1007/BF01231578
|
|
|||||
![\left [
\begin{smallmatrix}
\;\,\, 2&-3\\
-1&\;\,\, 2
\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/43d0e367343984e2cc0330bd6cf1e9d8.png)