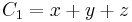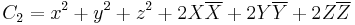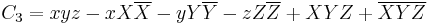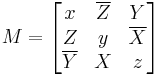F₄ (mathematics)

Group theory

Group theory
Basic notions Subgroup Normal subgroup Quotient group Group homomorphism (semi-)direct product
Finite groups (classification) Cyclic group Z_n Symmetric group, S_n Dihedral group, D_n Alternating group A_n Mathieu groups M₁₁, M₁₂, M₂₂, M₂₃, M₂₄ Conway groups Co₁, Co₂, Co₃ Janko groups J₁, J₂, J₃, J₄ Fischer groups F₂₂, F₂₃, F₂₄ Baby Monster group B Monster group M
Discrete groups and lattices The integers, Z Lattice (group) Modular groups, PSL(2,Z) and SL(2,Z)
Topological groups and Lie groups Solenoid (mathematics) Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) G₂ F₄ E₆ E₇ E₈ Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞)

Lie groups

Classical groups General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n)
Simple Lie groups List of simple Lie groups Infinite simple Lie groups: A_n, B_n, C_n, D_n, Exceptional simple Lie groups: G₂ F₄ E₆ E₇ E₈
Other Lie groups Circle group Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group
Lie algebras Exponential map Adjoint representation of a Lie group Adjoint representation of a Lie algebra Killing form Lie point symmetry
Structure of semi-simple Lie groups Dynkin diagrams Cartan subalgebra Root system Real form Complexification Split Lie algebra Compact Lie algebra
Representation theory Representation of a Lie group Representation of a Lie algebra
Lie groups in Physics Particle physics and representation theory Representation theory of the Lorentz group Representation theory of the Poincaré group Representation theory of the Galilean group

In mathematics, F₄ is the name of a Lie group and also its Lie algebra 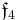$\mathfrak {f}_4$ . It is one of the five exceptional simple Lie groups. F₄ has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group is the trivial group. Its fundamental representation is 26-dimensional.

The compact real form of F₄ is the isometry group of a 16-dimensional Riemannian manifold known as the 'octonionic projective plane', OP². This can be seen systematically using a construction known as the magic square, due to Hans Freudenthal and Jacques Tits.

There are 3 real forms: a compact one, a split one, and a third one.

The F₄ Lie algebra may be constructed by adding 16 generators transforming as a spinor to the 36-dimensional Lie algebra so(9), in analogy with the construction of E₈.

In older books and papers, F₄ is sometimes denoted by E₄.

1 Algebra
2 Representations
3 See also
4 References

Algebra

Dynkin diagram

The Dynkin diagram for F₄ is given by or .

Weyl/Coxeter group

Its Weyl/Coxeter group is the symmetry group of the 24-cell: it is a solvable group of order 1152.

Cartan matrix

$\left [\begin{smallmatrix} 2&-1&0&0\\ -1&2&-2&0\\ 0&-1&2&-1\\ 0&0&-1&2 \end{smallmatrix}\right ]$

F₄ lattice

The F₄ lattice is a four dimensional body-centered cubic lattice (i.e. the union of two hypercubic lattices, each lying in the center of the other). They form a ring called the Hurwitz quaternion ring. The 24 Hurwitz quaternions of norm 1 form the 24-cell.

Roots of F₄

The 48 root vectors of F₄ can be found as the vertices of the 24-cell in two dual configurations:

24-cell vertices:

24 roots by (±1,±1,0,0), permutating coordinate positions

Dual 24-cell vertices:

8 roots by (±1, 0, 0, 0), permutating coordinate positions
16 roots by (±½, ±½, ±½, ±½).

Simple roots

One choice of simple roots for F₄ is given by the rows of the following matrix:

$\left [\begin{smallmatrix} 0&1&-1&0 \\ 0&0&1&-1 \\ 0&0&0&1 \\ \frac{1}{2}&-\frac{1}{2}&-\frac{1}{2}&-\frac{1}{2}\\ \end{smallmatrix}\right ]$

Hasse diagram

Graph of F4 Hasse diagram

F₄ polynomial invariant

Just as O(n) is the group of automorphisms which keep the quadratic polymials 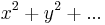$x^2%2By^2%2B...$ invariant, 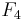$F_4$ is the group of automorphisms of the following set of 3 polynomials in 27 variables. (The first can easily be substituted into other two making 26 variables).

$C_1 = x%2By%2Bz$

$C_2 = x^2%2By^2%2Bz^2%2B2X\overline{X}%2B2Y\overline{Y}%2B2Z\overline{Z}$

$C_3 = xyz - xX\overline{X} - yY\overline{Y} - zZ\overline{Z} %2B XYZ %2B \overline{XYZ}$

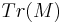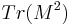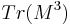Where x,y,z are real valued and X,Y,Z are octonion valued. Another way of writing these invariants is as (combinations of) $Tr(M)$ , $Tr(M^2)$ and $Tr(M^3)$ of the hermitian octonion matrix:

$M = \begin{bmatrix} x & \overline{Z} & Y \\ Z & y & \overline{X} \\ \overline{Y} & X & z \end{bmatrix}$

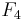$F_4$ is the only exceptional lie group which gives the automorphisms of a set of real commutative polynomials. (The other exceptional lie groups require anti-commutative polynomial invariants).

Representations

The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formula. The dimensions of the smallest irreducible representations are (sequence A121738 in OEIS):

1, 26, 52, 273, 324, 1053 (twice), 1274, 2652, 4096, 8424, 10829, 12376, 16302, 17901, 19278, 19448, 29172, 34749, 76076, 81081, 100776, 106496, 107406, 119119, 160056 (twice), 184756, 205751, 212992, 226746, 340119, 342056, 379848, 412776, 420147, 627912…

The 52-dimensional representation is the adjoint representation, and the 26-dimensional one is the trace-free part of the action of F₄ on the exceptional Albert algebra of dimension 27.

There are two non-isomorphic irreducible representations of dimensions 1053, 160056, 4313088, etc. The fundamental representations are those with dimensions 52, 1274, 273, 26 (corresponding to the four nodes in the Dynkin diagram in the order such that the double arrow points from the second to the third).

References

John Baez, The Octonions, Section 4.2: F₄, Bull. Amer. Math. Soc. 39 (2002), 145-205. Online HTML version at

http://math.ucr.edu/home/baez/octonions/node15.html.

Adams, J. Frank (1996), Lectures on exceptional Lie groups, Chicago Lectures in Mathematics, University of Chicago Press, ISBN 978-0-226-00526-3, MR 1428422, http://books.google.com/books?isbn=0226005275

Exceptional Lie groups

E₆ \| E₇ \| E₈ \| F₄ \| G₂

F4 (mathematics)

Contents