Fuzzy Pay-Off Method for Real Option Valuation
Fuzzy Pay-Off Method for Real Option Valuation (FPOM, or just Pay-off Method) [1] is a new method for valuing real options, created in 2008. It is based on the use of fuzzy logic and fuzzy numbers for the creation of the possible pay-off distribution of a project (real option). The structure of the method is similar to the probability theory based Datar-Mathews Method for Real Option Valuation.[2][3]
Contents |
Method
To understand the Fuzzy Pay-Off Method, it is worthwhile discussing it with reference to the Datar-Mathews Method (DM Method).
Under the DM Method, the option value is the expected value (mean) of all positive NPVs of the payoff distribution of the project in question. The Datar-Mathews method is shown to correspond to the answer from the Black–Scholes model when the same constraints are used. See further under "The Method" there.
- The payoff distribution is a probability distribution of project outcomes, generated using a simulation based on data (or estimates) provided by the responsible project manager.
- The probability weighted mean value: here the positive outcomes are multiplied by the probability of these positive outcomes (%) over all of the outcomes (100%).
- The answer is real option value.
- Formulaically:
![C_0 = E_0\left[Max\left(\tilde{S}_te^{-\mu\,\!t}-\tilde{X}_te^{-rt},0\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/53e2594e8eb5872d2ef4a84b8094eeb1.png)
- where
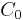 is the real option value ,
is the real option value , 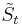 is a random variable representing the future benefits, or operating profits,
is a random variable representing the future benefits, or operating profits, 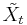 represents the strike price,
represents the strike price, 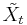 uses r, is the rate consistent with the risk of investment
uses r, is the rate consistent with the risk of investment
- where
By contrast, under the Fuzzy pay-off method, the real option value can be derived without any simulation whatsoever; the main observations of the model are the following:
- The fuzzy NPV of a project is (equal to) the pay-off distribution of a project value that is calculated with fuzzy numbers.
- The mean value of the positive values of the fuzzy NPV is the "possibilistic" mean value of the positive fuzzy NPV values.
- Real option value, ROV, calculated from the fuzzy NPV is the "possibilistic" mean value[4] of the positive fuzzy NPV values multiplied with the positive area of the fuzzy NPV over the total area of the fuzzy NPV.
- The real option formula can then be written simply as ROV = (A(Pos)/(A(Pos)+A(Neg)) x E[A+]
- where A(Pos) refers to the area of the positive part of the fuzzy distribution, A(Neg) refers to the area of the negative part of the fuzzy distribution, and E[A+] is the mean value of the positive part of the distribution. It can be seen that when the distribution is totally positive, the real options value reduces to the expected (mean) value, E[A+].
As can be seen, the real option value can be derived directly from the fuzzy NPV, without simulation.[5] At the same time, simulation is not an absolutely necessary step in the Datar-Mathews method, so the two methods are not very different in that respect. But what is totally different is that the Datar-Mathews method is based on probability theory and as such has a very different foundation from the pay-off method that is based on possibility theory. This means that the way the two models treat uncertainty is different.
Use of the method
The pay-off method for real option valuation is very easy to use compared to the previous real option valuation methods and it can be used with the most commonly used spreadsheet software without any add-ins. The method is useful in analyses for decision making regarding investments that have an uncertain future, and especially so if the underlying data is in the form of cash-flow scenarios. The method is less useful if optimal timing is the objective. The method is flexible and accommodates easily both one-stage investments and multi-stage investments (compound real options).
The method has been taken into use in some large international industrial companies for the valuation of research and development projects and portfolios.[6] In these analyses triangular fuzzy numbers are used. Other uses of the method so far are, for example, R&D project valuation IPR valuation, valuation of M&A targets and expected synergies,[7] valuation and optimization of M&A strategies, valuation of area development (construction) projects, valuation of large industrial real investments.
The use of the pay-off method is lately taught within the larger framework of real options, for example at the Lappeenranta University of Technology and at the Tampere University of Technology in Finland.
References
- ^ Collan, M., Fullér, R., and Mezei, J., 2009, Fuzzy Pay-Off Method for Real Option Valuation, Journal of Applied Mathematics and Decision Sciences, vol. 2009
- ^ Datar, V. & Mathews, S. 2004. European Real Options: An Intuitive Algorithm for the Black Scholes Formula. Journal of Applied Finance, 14(1)
- ^ Mathews, S. & Datar, V. 2007. A Practical Method for Valuing Real Options: The Boeing Approach. Journal of Applied Corporate Finance, 19(2): 95-104.
- ^ Fuller, R. & Majlender, P. 2003. On weighted possibilistic mean and variance of fuzzy numbers. Fuzzy Sets and Systems, 136: 363-374.
- ^ Collan, M., 2008, A New Method for Real Option Valuation Using Fuzzy Numbers, IAMSR Research Report, 7/2008
- ^ Heikkilä, M., 2009, Selection of R&D Portfolios of Real Options with Fuzzy Pay-offs under Bounded Rationality, IAMSR Research Report, 1/2009, ISBN 978-952-12-2316-7
- ^ Kinnunen, J., 2010, Valuing M&A Synergies as (Fuzzy) Real Options, 14th Annual International Conference on Real Options in Rome, Italy, June 16–19, 2010