Fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously[1] by Lotfi A. Zadeh[2] and Dieter Klaua[3] in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition — an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval [0, 1]. Fuzzy sets generalize classical sets, since the indicator functions of classical sets are special cases of the membership functions of fuzzy sets, if the latter only take values 0 or 1.[4] In fuzzy set theory, classical bivalent sets are usually called crisp sets. The fuzzy set theory can be used in a wide range of domains in which information is incomplete or imprecise, such as bioinformatics.[5]
Fuzzy sets can be applied, for example, to the field of genealogical research. When an individual is searching in vital records such as birth records for possible ancestors, the researcher must contend with a number of issues that could be encapsulated in a membership function.[6] Looking for an ancestor named John Henry Pittman, who you think was born in (probably eastern) Tennessee circa 1853 (based on statements of his age in later censuses, and a marriage record in Knoxville), what is the likelihood that a particular birth record for "John Pittman" is your John Pittman? What about a record in a different part of Tennessee for "J.H. Pittman" in 1851? (It has been suggested by Thayer Watkins[7] that Zadeh's ethnicity is an example of a fuzzy set)
Contents |
Definition
A fuzzy set is a pair 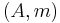 where
where  is a set and
is a set and ![m�: A \rightarrow [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/c72c91e5ebcbafaecc359957da052bd7.png) .
.
For each 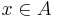 ,
, 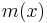 is called the grade of membership of
is called the grade of membership of  in
in 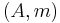 . For a finite set
. For a finite set 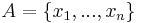 , the fuzzy set
, the fuzzy set 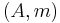 is often denoted by
is often denoted by 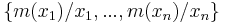 .
.
Let 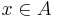 . Then
. Then  is called not included in the fuzzy set
is called not included in the fuzzy set 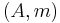 if
if 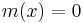 ,
,  is called fully included if
is called fully included if 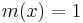 , and
, and  is called a fuzzy member if
is called a fuzzy member if 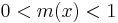 .[8] The set
.[8] The set 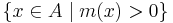 is called the support of
is called the support of 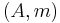 and the set
and the set 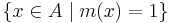 is called its kernel.
is called its kernel.
Sometimes, more general variants of the notion of fuzzy set are used, with membership functions taking values in a (fixed or variable) algebra or structure  of a given kind; usually it is required that
of a given kind; usually it is required that  be at least a poset or lattice. These are usually called L-fuzzy sets, to distinguish them from those valued over the unit interval. The usual membership functions with values in [0, 1] are then called [0, 1]-valued membership functions. These kinds of generalizations were first considered in 1967 by Joseph Goguen, who was a student of Zadeh.[9]
be at least a poset or lattice. These are usually called L-fuzzy sets, to distinguish them from those valued over the unit interval. The usual membership functions with values in [0, 1] are then called [0, 1]-valued membership functions. These kinds of generalizations were first considered in 1967 by Joseph Goguen, who was a student of Zadeh.[9]
Fuzzy logic
As an extension of the case of multi-valued logic, valuations (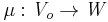 ) of propositional variables (
) of propositional variables (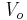 ) into a set of membership degrees (
) into a set of membership degrees (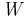 ) can be thought of as membership functions mapping predicates into fuzzy sets (or more formally, into an ordered set of fuzzy pairs, called a fuzzy relation). With these valuations, many-valued logic can be extended to allow for fuzzy premises from which graded conclusions may be drawn.[10]
) can be thought of as membership functions mapping predicates into fuzzy sets (or more formally, into an ordered set of fuzzy pairs, called a fuzzy relation). With these valuations, many-valued logic can be extended to allow for fuzzy premises from which graded conclusions may be drawn.[10]
This extension is sometimes called "fuzzy logic in the narrow sense" as opposed to "fuzzy logic in the wider sense," which originated in the engineering fields of automated control and knowledge engineering, and which encompasses many topics involving fuzzy sets and "approximated reasoning."[11]
Industrial applications of fuzzy sets in the context of "fuzzy logic in the wider sense" can be found at fuzzy logic.
Fuzzy number
A fuzzy number is a convex, normalized fuzzy set 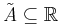 whose membership function is at least segmentally continuous and has the functional value
whose membership function is at least segmentally continuous and has the functional value 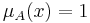 at precisely one element.
at precisely one element.
This can be likened to the funfair game "guess your weight," where someone guesses the contestant's weight, with closer guesses being more correct, and where the guesser "wins" if he or she guesses near enough to the contestant's weight, with the actual weight being completely correct (mapping to 1 by the membership function).
Fuzzy interval
A fuzzy interval is an uncertain set 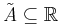 with a mean interval whose elements possess the membership function value
with a mean interval whose elements possess the membership function value 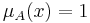 . As in fuzzy numbers, the membership function must be convex, normalized, at least segmentally continuous.[12]
. As in fuzzy numbers, the membership function must be convex, normalized, at least segmentally continuous.[12]
Fuzzy relation equation
The fuzzy relation equation is an equation of the form A · R = B, where A and B are fuzzy sets, R is a fuzzy relation, and A · R stands for the composition of A with R.
See also
References
- ^ Michael Winter (2007). Goguen categories: a categorical approach to L-fuzzy relations. Springer. p. ix. ISBN 9781402061639. http://books.google.com/books?id=5wy_tope2VEC&pg=PR9.
- ^ L. A. Zadeh (1965) "Fuzzy sets". Information and Control 8 (3) 338–353.
- ^ Klaua, D. (1965) Über einen Ansatz zur mehrwertigen Mengenlehre. Monatsb. Deutsch. Akad. Wiss. Berlin 7, 859–867. A recent in-depth analysis of this paper has been provided by Gottwald, S. (2010). "An early approach toward graded identity and graded membership in set theory". Fuzzy Sets and Systems 161 (18): 2369–2379. doi:10.1016/j.fss.2009.12.005. preprint
- ^ D. Dubois and H. Prade (1988) Fuzzy Sets and Systems. Academic Press, New York.
- ^ Lily R. Liang, Shiyong Lu, Xuena Wang, Yi Lu, Vinay Mandal, Dorrelyn Patacsil, and Deepak Kumar, “FM-test: A Fuzzy-Set-Theory-Based Approach to Differential Gene Expression Data Analysis”, BMC Bioinformatics, 7 (Suppl 4): S7. 2006.
- ^ H. Bandemer, "Fuzzy Local Inference in Fuzzy Knowledge Bases" in V. Novak, J. Ramik, M. Mares, M. Cerny, J. Nekola (eds.), Fuzzy Approach to Reasoning and Decision-Making, 1990, Bechyne, Czechoslovakia, 47-48. [1]
- ^ "Fuzzy Logic: The Logic of Fuzzy Sets"
- ^ AAAI http://www.aaai.org/aitopics/pmwiki/pmwiki.php/AITopics/FuzzyLogic
- ^ Goguen, Joseph A., 1967, "L-fuzzy sets". Journal of Mathematical Analysis and Applications 18: 145–174
- ^ Siegfried Gottwald, 2001. A Treatise on Many-Valued Logics. Baldock, Hertfordshire, England: Research Studies Press Ltd., ISBN 978-0863802621
- ^ "The concept of a linguistic variable and its application to approximate reasoning," Information Sciences 8: 199–249, 301–357; 9: 43–80.
- ^ "Fuzzy sets as a basis for a theory of possibility," Fuzzy Sets and Systems 1: 3–28
Further reading
- George J. Klir; Bo Yuan (1995). Fuzzy sets and fuzzy logic: theory and applications. Prentice Hall. ISBN 9780131011717.
- Hans-Jürgen Zimmermann (2001). Fuzzy set theory—and its applications (4th ed.). Kluwer. ISBN 9780792374350.
- Didier Dubois, Henri M. Prade, ed (2000). Fundamentals of fuzzy sets. The Handbooks of Fuzzy Sets Series. 7. Springer. ISBN 9780792377320.
- Ulrich Höhle, Stephen Ernest Rodabaugh, ed (1999). Mathematics of fuzzy sets: logic, topology, and measure theory. The Handbooks of Fuzzy Sets Series. 3. Springer. ISBN 9780792383888.
- Gottwald, S. (2006). "Universes of Fuzzy Sets and Axiomatizations of Fuzzy Set Theory. Part I: Model-Based and Axiomatic Approaches". Studia Logica 82 (2): 211–244. doi:10.1007/s11225-006-7197-8. preprint. . Gottwald, S. (2006). "Universes of Fuzzy Sets and Axiomatizations of Fuzzy Set Theory. Part II: Category Theoretic Approaches". Studia Logica 84: 23–50. doi:10.1007/s11225-006-9001-1. preprint. .
External links
- Uncertainty model Fuzziness
- Fuzzy Systems Journal http://www.elsevier.com/wps/find/journaldescription.cws_home/505545/description#description
- ScholarPedia [2]
- The Algorithm of Fuzzy Analysis
- Fuzzy Image Processing