Frontogenesis

Frontogenesis, in meteorology, refers to the formation or strengthening of an atmospheric front. During frontogenesis, the temperature gradient tightens and as a result the thermal wind becomes imbalanced. To maintain balance, the geostrophic wind aloft and below adjust, such that regions of divergence/convergence form. Mass continuity would require a vertical transport of air along the cold front where there is divergence (lowered pressure). Although this circulation is described by a series of processes, they are actually occurring at the same time, observable along the front as a thermally direct circulation. There are several factors that influence the final shape and tilt of the circulation around the front, ultimately determining the type and location of clouds and precipitation. ^[1]^[2]

3-Dimensional Equation

The three-dimensional form of the frontogenesis equation is

$\begin{alignat}{3} F = \frac{1}{|\nabla \theta|}\cdot \frac{\partial \theta}{\partial x}\left \{ \frac{1}{C_p} \left ( \frac{p_\circ}{p} \right )^\kappa \left [ \frac{\partial}{\partial x} \left (\frac{dQ}{dt} \right ) \right ] - \left ( \frac{\partial u}{\partial x} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial x} \frac{\partial \theta}{\partial y} \right ) - \left ( \frac{\partial w}{\partial x} \frac{\partial \theta}{\partial z} \right ) \right \} \\ %2B \frac{\partial \theta}{\partial y}\left \{ \frac{1}{C_p} \left ( \frac{p_\circ}{p} \right )^\kappa \left [ \frac{\partial}{\partial y} \left (\frac{dQ}{dt} \right ) \right ] - \left ( \frac{\partial u}{\partial y} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial y} \frac{\partial \theta}{\partial y} \right ) - \left ( \frac{\partial w}{\partial y} \frac{\partial \theta}{\partial z} \right ) \right \} \\ %2B \frac{\partial \theta}{\partial z}\left \{ \frac{p_\circ^\kappa}{C_p} \left [ \frac{\partial}{\partial z} \left (p^{-\kappa} \frac{dQ}{dt} \right ) \right ] - \left ( \frac{\partial u}{\partial z} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial z} \frac{\partial \theta}{\partial y} \right ) - \left ( \frac{\partial w}{\partial z} \frac{\partial \theta}{\partial z} \right ) \right \}\end{alignat}$

where each dimension begins with a diabatic term; in the $x$ direction

$\frac{1}{C_p} \left ( \frac{p_\circ}{p} \right )^\kappa \left [ \frac{\partial}{\partial x} \left (\frac{dQ}{dt} \right ) \right ]$

in the $y$ direction

$\frac{1}{C_p} \left ( \frac{p_\circ}{p} \right )^\kappa \left [ \frac{\partial}{\partial y} \left (\frac{dQ}{dt} \right ) \right ]$

and in the $z$ direction

$\frac{p_\circ^\kappa}{C_p} \left [ \frac{\partial}{\partial z} \left (p^{-\kappa} \frac{dQ}{dt} \right ) \right ]$ .

The equation also includes horizontal and vertical deformation terms; in the $x$ direction

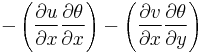
$-\left ( \frac{\partial u}{\partial x} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial x} \frac{\partial \theta}{\partial y} \right )$

and in the $y$ direction

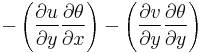
$-\left ( \frac{\partial u}{\partial y} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial y} \frac{\partial \theta}{\partial y} \right )$

and in the vertical $z$ direction

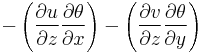$-\left ( \frac{\partial u}{\partial z} \frac{\partial \theta}{\partial x} \right ) - \left ( \frac{\partial v}{\partial z} \frac{\partial \theta}{\partial y} \right )$ .

The final terms are the tilting term and the vertical divergence term; the tilting term is represented in the three-dimensional frontogenesis equation in the $x$ and $y$ directions

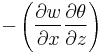
$-\left ( \frac{\partial w}{\partial x} \frac{\partial \theta}{\partial z} \right )$

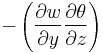
$-\left ( \frac{\partial w}{\partial y} \frac{\partial \theta}{\partial z} \right )$

and the vertical divergence term is present as

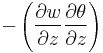
$-\left ( \frac{\partial w}{\partial z} \frac{\partial \theta}{\partial z} \right )$

References

^ Preview Text, Holton, James R., 2004: An Introduction to Dynamic Meteorology. Academic Press, 277 pp.
^ Preview Text, Carlson, Toby N., 1991: Mid-Latitude Weather Systems. HarperCollins, 435 pp.

Frontogenesis

3-Dimensional Equation

References

See also