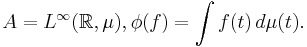Free independence
In the mathematical theory of free probability, the notion of free independence was introduced by Dan Voiculescu[1]. The definition of free independence is parallel to the classical definition of independence, except that the role of Cartesian products of measure spaces (corresponding to tensor products of their function algebras) is played by the notion of a free product of (non-commutative) probability spaces.
In the context of Voiculescu's free probability theory, many classical-probability theorems or phenomena have free probability analogs: the same theorem or phenomenon holds (perhaps with slight modifications) if the classical notion of independence is replaced by free independence. Examples of this include: the free central limit theorem; notions of free convolution; existence of free stochastic calculus and so on.
Let 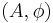 be a non-commutative probability space, i.e. a unital algebra
be a non-commutative probability space, i.e. a unital algebra  over
over  equipped with a unital linear functional
equipped with a unital linear functional 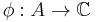 . As an example, one could take, for a probability measure
. As an example, one could take, for a probability measure  ,
,
Another example may be 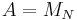 , the algebra of
, the algebra of 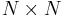 matrices with the functional given by the normalized trace
matrices with the functional given by the normalized trace 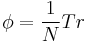 . Even more generally,
. Even more generally,  could be a von Neumann algebra and
could be a von Neumann algebra and  a state on
a state on  . A final example is the group algebra
. A final example is the group algebra 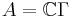 of a (discrete) group
of a (discrete) group  with the functional
with the functional  given by the group trace
given by the group trace 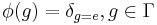 .
.
Let 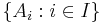 be a family of unital subalgebras of
be a family of unital subalgebras of  .
.
Definition. The family 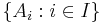 is called freely independent if
is called freely independent if  whenever
whenever 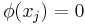 ,
, 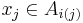 and
and 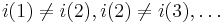 .
.
If 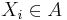 ,
, 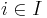 is a family of elements of
is a family of elements of  (these can be thought of as random variables in
(these can be thought of as random variables in  ), they are called
), they are called
freely independent if the algebras 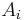 generated by
generated by 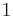 and
and 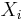 are freely independent.
are freely independent.
Examples of free independence
- Let
 be the free product of groups
be the free product of groups 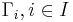 , let
, let 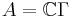 be the group algebra,
be the group algebra, 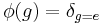 be the group trace, and set
be the group trace, and set 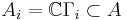 . Then
. Then 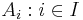 are freely independent.
are freely independent.
- Let
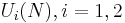 be
be 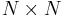 unitary random matrices, taken independently at random from the
unitary random matrices, taken independently at random from the 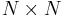 unitary group (with respect to the Haar measure). Then
unitary group (with respect to the Haar measure). Then 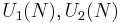 become asymptotically freely independent as
become asymptotically freely independent as 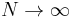 . (Asymptotic freeness means that the definition of freeness holds in the limit as
. (Asymptotic freeness means that the definition of freeness holds in the limit as 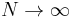 ).
).
- More generally, independent random matrices tend to be asymptotically freely independent, under certain conditions.
References
- ^ D. Voiculescu, K. Dykema, A. Nica, "Free Random Variables", CIRM Monograph Series, AMS, Providence, RI, 1992