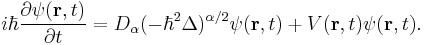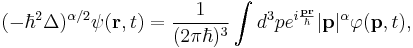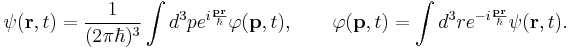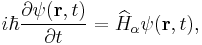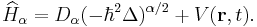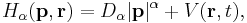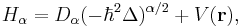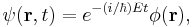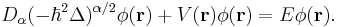Fractional Schrödinger equation

The fractional Schrödinger equation is a fundamental equation of fractional quantum mechanics. It was discovered by Nick Laskin (1999) as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by Nick Laskin^[1]. The fractional Schrödinger equation has the following form ^[2]:

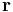$i\hbar \frac{\partial \psi (\mathbf{r},t)}{\partial t}=D_\alpha (-\hbar ^2\Delta )^{\alpha /2}\psi (\mathbf{r},t)%2BV(\mathbf{r},t)\psi (\mathbf{r},t).$

Here $\mathbf{r}$ is a 3-dimensional vector, 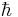$\hbar$ is the Planck constant, 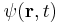$\psi(\mathbf{r},t)$ is the wavefunction, which is the quantum mechanical probability amplitude for the particle to have a given position 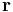$\mathbf{r}$ at any given time t, 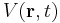$V(\mathbf{r},t)$ is a potential energy, and 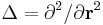$\Delta =\partial ^2/\partial \mathbf{r}^2$ is the Laplace operator. 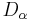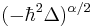Further, $D_\alpha$ is a scale constant with physical dimension $[D_\alpha ]=\mathrm{erg}^{1-\alpha }\cdot \mathrm{cm}^\alpha \cdot \mathrm{sec}^{-\alpha }$ , (at α = 2, D₂ =1/2m, where m is a particle mass), and the operator $(-\hbar ^2\Delta )^{\alpha /2}$ is the 3-dimensional fractional quantum Riesz derivative defined by

$(-\hbar ^2\Delta )^{\alpha /2}\psi (\mathbf{r},t)=\frac 1{(2\pi \hbar )^3}\int d^3pe^{i\frac{\mathbf{pr}}\hbar }|\mathbf{p}|^\alpha \varphi ( \mathbf{p},t),$

Here the wave functions in the space 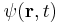$\psi(\mathbf{r},t)$ and momentum 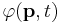$\varphi (\mathbf{p},t)$ representations are related each other by the 3-dimensional Fourier transforms

$\psi (\mathbf{r},t)=\frac 1{(2\pi \hbar )^3}\int d^3pe^{i\frac{\mathbf{pr}} \hbar }\varphi (\mathbf{p},t),\qquad \varphi (\mathbf{p},t)=\int d^3re^{-i \frac{\mathbf{pr}}\hbar }\psi (\mathbf{r},t).$

The index α in the fractional Schrödinger equation is the Lévy index, 1 < α ≤ 2. Thus, the fractional Schrödinger equation includes a space derivative of fractional order α instead of the second order (α = 2) space derivative in the standard Schrödinger equation. Thus, the fractional Schrödinger equation is a fractional differential equation in accordance with modern terminology^[3]. This is the main point of the term fractional Schrödinger equation or a more general term fractional quantum mechanics^[4]. At α = 2 fractional Schrödinger equation becomes the well-known Schrödinger equation.

The fractional Schrödinger equation has the following operator form

$i\hbar \frac{\partial \psi (\mathbf{r},t)}{\partial t}=\widehat{H}_\alpha \psi (\mathbf{r},t),$

where the fractional Hamilton operator 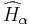$\widehat{H}_\alpha$ is given by

$\widehat{H}_\alpha =D_\alpha (-\hbar ^2\Delta )^{\alpha /2}%2BV(\mathbf{r},t).$

The Hamilton operator, 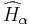$\widehat{H}_\alpha$ corresponds to classical mechanics Hamiltonian function

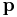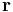$H_\alpha (\mathbf{p},\mathbf{r})=D_\alpha |\mathbf{p}|^\alpha %2BV(\mathbf{r},t),$

where $\mathbf{p}$ and $\mathbf{r}$ are the momentum and the coordinate respectively.

Time-independent fractional Schrödinger equation

The special case when the Hamiltonian 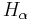$H_\alpha$ is independent of time

$H_\alpha =D_\alpha (-\hbar ^2\Delta )^{\alpha /2}%2BV(\mathbf{r}),$

is of great importance for physical applications. It is easy to see that in this case there exist the special solution of the fractional Schrödinger equation

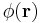$\psi (\mathbf{r},t)=e^{-(i/\hbar )Et}\phi (\mathbf{r}),$

where $\phi (\mathbf{r})$ satisfies

$H_\alpha \phi (\mathbf{r}) = E\phi (\mathbf{r}),$

$D_\alpha (-\hbar ^2\Delta )^{\alpha /2}\phi (\mathbf{r})%2BV(\mathbf{r})\phi ( \mathbf{r})=E\phi (\mathbf{r}).$

This is the time-independent fractional Schrödinger equation.

Thus, we see that the wave function 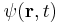$\psi (\mathbf{r},t)$ oscillates with a definite frequency. In classical physics the frequency corresponds to the energy. Therefore, the quantum mechanical state has a definite energy E. The probability to find a particle at 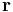$\mathbf{r}$ is the absolute square of the wave function 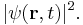$| \psi (\mathbf{r},t) |^2 .$ Because of time-independent fractional Schrödinger equation this is equal to 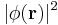$| \phi (\mathbf{r})|^2$ and does not depend upon the time. That is, the probability of finding the particle at $\mathbf{r}$ is independent of the time. One can say that the system is in a stationary state. In other words, there is no variation in the probabilities as a function of time.

References

^ N. Laskin, (2000), Fractional Quantum Mechanics and Lévy Path Integrals. Physics Letters 268A, 298-304.
^ N. Laskin, (2002), Fractional Schrödinger equation, Physical Review E66, 056108 [7 pages]. (also available online: http://arxiv.org/abs/quant-ph/0206098)
^ S. G. Samko, A. A. Kilbas, and O. I. Marichev, Fractional Integrals and Derivatives, Theory and Applications ~Gordon and Breach, Amsterdam, 1993
^ N. Laskin, (2000), Fractional Quantum Mechanics, Physical Review E62, 3135-3145. (also available online: http://arxiv.org/abs/0811.1769)

Branches of physics

Fractional Schrödinger equation

Time-independent fractional Schrödinger equation

See also

References