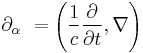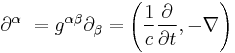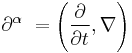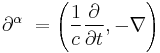Four-gradient

The four-gradient is the four-vector generalization of the gradient:

$\partial_\alpha \ = \left(\frac{1}{c} \frac{\partial}{\partial t}, \nabla \right)$

and where g^αβ is the metric tensor, which here has been chosen for flat spacetime with the signature [ + - - - ]

$\partial^\alpha \ = g^{\alpha \beta} \partial_\beta = \left(\frac{1}{c} \frac{\partial}{\partial t}, -\nabla \right)$

and is sometimes also represented as D.

The square of D is the four-Laplacian, which is called the d'Alembert operator:

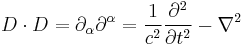$D\cdot D = \partial_\alpha \partial^\alpha = \frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \nabla^2$ .

As it is the dot product of two four-vectors, the d'Alembertian is a Lorentz invariant scalar.

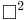Occasionally, in analogy with the 3-dimensional notation, the symbols $\Box$ and $\Box^2$ are used for the 4-gradient and d'Alembertian respectively. More commonly however, the symbol $\Box$ is reserved for the d'Alembertian.

Derivation

In 3 dimensions, the gradient operator maps a scalar field to a vector field such that the line integral between any two points in the vector field is equal to the difference between the scalar field at these two points. Based on this, it may appear that the natural extension of the gradient to four dimensions should be:

$\partial^\alpha \ = \left( \frac{\partial}{\partial t}, \nabla \right)$

However, a line integral involves the application of the vector dot product, and when this is extended to four dimensional space-time, a change of sign is introduced to either the spacial co-ordinates or the time co-ordinate depending on the convention used. This is due to the non-Euclidean nature of space-time. In this article, we place a negative sign on the spatial co-ordinates. In addition to the change of sign, a factor of c must be introduced due to the different units being used to measure space and time. Adding these two corrections to the above expression gives the correct definition of four-gradient:

$\partial^\alpha \ = \left(\frac{1}{c} \frac{\partial}{\partial t}, -\nabla \right)$

References

S. Hildebrandt, "Analysis II" (Calculus II), ISBN 3-540-43970-6, 2003
L.C. Evans, "Partial differential equations", A.M.Society, Grad.Studies Vol.19, 1988
J.D. Jackson, "Classical Electrodynamics" Chapter 11, Wiley ISBN 0-471-30932-X