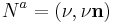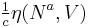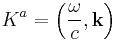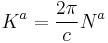Four-frequency
The four-frequency of a photon is defined by
where  is the photon's frequency and
is the photon's frequency and 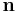 is a unit vector in the direction of the photon's motion. The four-frequency is always a future-pointing and null vector. An observer moving with four-velocity
is a unit vector in the direction of the photon's motion. The four-frequency is always a future-pointing and null vector. An observer moving with four-velocity  will observe a frequency
will observe a frequency
Where 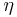 is the Minkowski inner-product (+---)
is the Minkowski inner-product (+---)
Closely related to the four-frequency is the wave four-vector defined by
where 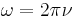 ,
,  is the speed of light and
is the speed of light and 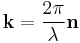 and
and  is the wavelength of the photon. The wave four-vector is more often used in practice than the four-frequency, but the two vectors are related (using
is the wavelength of the photon. The wave four-vector is more often used in practice than the four-frequency, but the two vectors are related (using 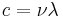 ) by
) by
References
- Woodhouse, N.M.J. (2003). Special Relativity. London: Springer-Verlag. ISBN 1852334266.