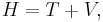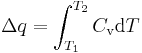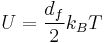Forms of energy

In the context of physical sciences, several forms of energy have been defined. These include:

Thermal energy, thermal energy in transit is called heat
Chemical energy
Electric energy
Radiant energy, the energy of electromagnetic radiation
Nuclear energy
Magnetic energy
Elastic energy
Sound energy
Mechanical energy
Luminous energy
Mass (E=mc²)

These forms of energy may be divided into two main groups; kinetic energy and potential energy. Other familiar types of energy are a varying mix of both potential and kinetic energy.

Energy may be transformed between these forms, some with 100% energy conversion efficiency and others with less. Items that transform between these forms are called transducers.

The above list of the known possible forms of energy is not necessarily complete. Whenever physical scientists discover that a certain phenomenon appears to violate the law of energy conservation, new forms may be added, as is the case with dark energy, a hypothetical form of energy that permeates all of space and tends to increase the rate of expansion of the universe.

Classical mechanics distinguishes between potential energy, which is a function of the position of an object, and kinetic energy, which is a function of its movement. Both position and movement are relative to a frame of reference, which must be specified: this is often (and originally) an arbitrary fixed point on the surface of the Earth, the terrestrial frame of reference. It has been attempted to categorize all forms of energy as either kinetic or potential: this is not incorrect, but neither is it clear that it is a real simplification, as Feynman points out:

These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopic potential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.

Examples of the interconversion of energy
Mechanical energy is converted
into	by
Mechanical energy	Lever
Thermal energy	Brakes
Electric energy	Dynamo
Electromagnetic radiation	Synchrotron
Chemical energy	Matches
Nuclear energy	Particle accelerator

1 Mechanical energy
2 Mechanical work
3 Potential energy
4 Elastic potential energy
5 Kinetic energy
6 Surface energy
7 Sound energy
8 Gravitational potential energy
9 Thermal energy
10 Electric energy
11 Chemical energy
12 Nuclear energy
13 References

Mechanical energy

Main article: Mechanical energy

General non-relativistic mechanics

Mechanical energy (symbols E_M or E) manifest in many forms, but can be broadly classified into potential energy (E_p, V, U or Φ) and kinetic energy (E_k or T). The term potential energy is a very general term, because it exists in all force fields, such as gravitation, electrostatic and magnetic fields. Potential energy refers to the energy any object gains due to its position in a force field.

The relation between mechanical energy with kinetic and potential energy is simply

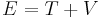$E = T %2B V \,\!$ .

Lagrangian and Hamiltonian mechanics

In more advanced topics, kinetic plus potential energy is physically the total energy of the system, but also known as the Hamiltonian of the system:

$H = T %2B V , \,\!$

used in Hamilton's equations of motion, to obtain equations describing a classical system in terms of energy rather than forces. The Hamiltonian is just a mathematical expression, rather than a form of energy.

Another analogous quantity of profound applicability and efficiency is the Lagrangian of the system:

$L = T - V \,\!$ ,

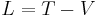used in Lagrange's equations of motion, which serve the same purpose as Hamilton's equations.

Mechanical work

Main article: Work (physics)

Translational motion

If F is the force and r is the displacement, then the change in mechanical work done along the path between positions r₁ and r₂ due to the force is, in integral form:

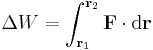$\Delta W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F}\cdot\mathrm{d}\mathbf{r}$ ,

(the dot represents the scalar product of the two vectors). The general equation above can be simplified in a number of common cases, notably when dealing with gravity or with elastic forces. If the force is conservative the equation can be written in differential form as

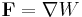$\mathbf{F} = \nabla W$ .

Rotational motion

The rotational analogue is the work done by a torque τ, between the angles θ₁ and θ₂,

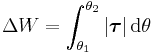$\Delta W = \int_{\theta_1}^{\theta_2} \left | \boldsymbol{\tau} \right | \mathrm{d}\theta$ .

Potential energy

Main article: Potential energy

Potential energy is defined as the work done against a given force in changing the position of an object with respect to a reference position, often taken to be infinite separation. In other words it is the work done on the object to give it that much energy. Changes in work and potential energy are related simply,

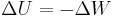$\Delta U = -\Delta W$ .

The name "potential" energy originally signified the idea that the energy could readily be transferred as work — at least in an idealized system (reversible process, see below). This is not completely true for any real system, but is often a reasonable first approximation in classical mechanics.

Elastic potential energy

Main article: Elastic potential energy

Elastic potential energy is defined as a work needed to compress or extend a spring. The tension/compression force F in a spring or any other system which obeys Hooke's law is proportional to the extension/compression x,

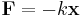$\mathbf{F} = -k\mathbf{x}\,\!$ ,

where k is the force constant of the particular spring or system. In this case the force is conservative, the calculated work becomes

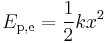$E_\mathrm{p,e} = \frac{1}{2}kx^2\,\!$ .

If k is not constant the above equation will fail. Hooke's law is a good approximation for behaviour of chemical bonds under stable conditions, i.e. when they are not being broken or formed.

Kinetic energy

Main article: Kinetic energy

General scope

Kinetic energy is the work required to accelerate an object to a given speed. These values are expressed as:

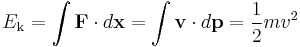
$E_\mathrm{k} = \int \mathbf{F} \cdot d \mathbf{x} = \int \mathbf{v} \cdot d \mathbf{p}= \frac{1}{2}mv^2\,\!$

Special Relativistic mechanics

At speeds approac hing the speed of light, c, this work must be calculated using Lorentz transformations, and applying mass and energy conservation, which results in the following:

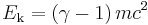
$E_\mathrm{k} = \left ( \gamma - 1 \right ) m c^2 \,\!$

where 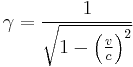$\gamma = \frac{1}{\sqrt{1 - \left ( \frac{v}{c} \right )^2}} \,\!$ is the lorentz factor.

Here the two terms on the right hand side are identified with the total energy and the rest energy of the object, respectively. This equation reduces to the one above it, at small (compared to c) speed. The kinetic energy is zero at v=0 (when γ = 1), so that at rest, the total energy is the rest energy. So a mass at rest in some inertial reference frame has a corresponding amount of rest energy equal to:

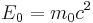
$E_0 = m_0 c^2 \,\!$

All masses at rest have a tremendous amuont of energy, due to the proportionality factor of c².

Surface energy

If there is any kind of tension in a surface, such as a stretched sheet of rubber or material interfaces, it is possible to define surface energy.

If γ is the surface tension, and S = surface area, then the work done W to increase the area by a unit area is the surface energy:

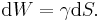
$\mathrm{d}W = \gamma \mathrm{d}S . \,\!$

In particular, any meeting of dissimilar materials that do not mix will result in some kind of surface tension, if there is freedom for the surfaces to move then, as seen in capillary surfaces for example, the minimum energy will as usual be sought.

A minimal surface, for example, represents the smallest possible energy that a surface can have if its energy is proportional to the area of the surface. For this reason, (open) soap films of small size are minimal surfaces (small size reduces gravity effects, and openness prevents pressure from building up. Note that a bubble is a minimum energy surface but not a minimal surface by definition).

Sound energy

Sound is a form of mechanical vibration which propagates through any mechanical medium. It is closely related to the ability of the human ear to perceive sound. The wide outer area of the ear is maximized to collect sound vibrations. It is amplified and passed through the outer ear, striking the eardrum, which transmits sounds into the inner ear. Auditory nerves fire according to the particular vibrations of the sound waves in the inner ear, which designate such things as the pitch and volume of the sound. The ear is set up in an optimal way to interpret sound energy in the form of vibrations.

Gravitational potential energy

Main article: Gravitational potential energy

The gravitational force very near the surface of a massive body (e.g. a planet) varies very little with small changes in height, h, and locally is equal mg where m is mass, and g is the gravitational acceleration (AKA field strength). At the Earth's surface g = 9.81 m s^-1. In these cases, the gravitational potential energy is given by

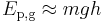
$E_\mathrm{p,g} \approx mgh\,\!$

A more general expression for the potential energy due to Newtonian gravitation between two bodies of masses m₁ and m₂, is

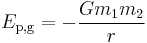$E_\mathrm{p,g} = -\frac{G m_1 m_2}{r}\,\!$ ,

where r is the separation between the two bodies and G is the gravitational constant, 6.6742(10) × 10^-11 m³ kg^-1 s^-2.^[1] In this case, the zero potential reference point is the infinite separation of the two bodies. Care must be taken that these masses are point masses or uniform spherical solids/shells. It cannot be applied directly to any objects of any shape and any mass.

In terms of the gravitational potential (Φ, U or V), the potential energy is (by definition of gravitational potential),

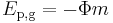$E_\mathrm{p,g} = -\Phi m \,\!$ .

Thermal energy

Examples of the interconversion of energy
Thermal energy is converted
into	by
Mechanical energy	Steam turbine
Thermal energy	Heat exchanger
Electric energy	Thermocouple
Electromagnetic radiation	Hot objects
Chemical energy	Blast furnace
Nuclear energy	Supernova

Main article: Thermal energy

General scope

Thermal energy (of some state of matter - gas, plasma, solid, etc.) is the energy associated with the microscopical random motion of particles constituting the media. For example, in case of monoatomic gas it is just a kinetic energy of motion of atoms of gas as measured in the reference frame of the center of mass of gas. In case of molecules in the gas rotational and vibrational energy is involved. In the case of liquids and solids there is also potential energy (of interaction of atoms) involved, and so on.

A heat is defined as a transfer (flow) of thermal energy across certain boundary (for example, from a hot body to cold via the area of their contact. A practical definition for small transfers of heat is

$\Delta q = \int_{T_1}^{T_2} C_\mathrm{v}\mathrm{d}T$

where C_v is the heat capacity of the system. This definition will fail if the system undergoes a phase transition—e.g. if ice is melting to water—as in these cases the system can absorb heat without increasing its temperature. In more complex systems, it is preferable to use the concept of internal energy rather than that of thermal energy (see Chemical energy below).

Despite the theoretical problems, the above definition is useful in the experimental measurement of energy changes. In a wide variety of situations, it is possible to use the energy released by a system to raise the temperature of another object, e.g. a bath of water. It is also possible to measure the amount of electric energy required to raise the temperature of the object by the same amount. The calorie was originally defined as the amount of energy required to raise the temperature of one gram of water by 1 °C (approximately 4.1855 J, although the definition later changed), and the British thermal unit was defined as the energy required to heat one pound of water by 1 °F (later fixed as 1055.06 J).

Kinetic theory

In kinetic theory which describes the ideal gas, the thermal energy per degree of freedom is given by:

$U = \frac{d_f}{2}k_B T$

where d_f is the number of degrees of freedom and ksub>B is the Boltzmann constant. The total themeral energies would equal the total internal energy of the gas, since intermolecular potential energy is neglected in this theory. The term k_BT occurs very frequently into statistical thermodynamics.

Electric energy

Main articles: Electromagnetism and Electricity

Examples of the interconversion of energy
Electric energy is converted
into	by
Mechanical energy	Electric motor
Thermal energy	Resistor
Electric energy	Transformer
Electromagnetic radiation	Light-emitting diode
Chemical energy	Electrolysis
Nuclear energy	Synchrotron

Electrostatic energy

General scope

The electric potential energy of given configuration of charges is defined as the work which must be done against the Coulomb force to rearrange charges from infinite separation to this configuration (or the work done by the Coulomb force separating the charges from this configuration to infinity). For two point-like charges Q₁ and Q₂ at a distance r this work, and hence electric potential energy is equal to:

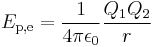
$E_\mathrm{p,e} = \frac{1}{{4\pi\epsilon_0}}{{Q_1Q_2}\over{r}}$

where ε₀ is the electric constant of a vacuum, 10⁷/4πc₀² or 8.854188… × 10⁻¹² F m⁻¹.^[1] In terms of electrostatic potential (ϕ for absolute, V for differance in potential), again by definition, electrostatic potential energy is given by:

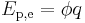$E_\mathrm{p,e} = \phi q \,\!$ .

If the charge is accumulated in a capacitor (of capacitance C), the reference configuration is usually selected not to be infinite separation of charges, but vice versa - charges at an extremely close proximity to each other (so there is zero net charge on each plate of a capacitor). The justification for this choice is purely practical - it is easier to measure both voltage difference and magnitude of charges on a capacitor plates not versus infinite separation of charges but rather versus discharged capacitor where charges return to close proximity to each other (electrons and ions recombine making the plates neutral). In this case the work and thus the electric potential energy becomes

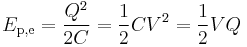$E_\mathrm{p,e} = \frac{Q^2}{2C} = \frac{1}{2}CV^2 = \frac{1}{2}VQ \,\!$ ,

(different forms obtained using the definition of capacitance).

Electric energy

Main article: Electric energy

Electric circuits

If an electric current passes through a resistor, electric energy is converted to heat; if the current passes through an electric appliance, some of the electric energy will be converted into other forms of energy (although some will always be lost as heat). The amount of electric energy due to an electric current can be expressed in a number of different ways:

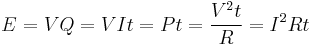
$E = VQ = VIt = Pt = \frac{V^2 t}{R} = {I^2}Rt \,\!$

where V is the electric potential difference (in volts), Q is the charge (in coulombs), I is the current (in amperes), t is the time for which the current flows (in seconds), P is the power (in watts) and R is the electric resistance (in ohms). The last of these expressions is important in the practical measurement of energy, as potential difference, resistance and time can all be measured with considerable accuracy.

Magnetic energy

Main article: Magnetic energy

General scope

There is no fundamental difference between magnetic energy and electric energy: the two phenomena are related by Maxwell's equations. The potential energy of a magnet of magnetic moment m in a magnetic field B is defined as the work of magnetic force (actually of magnetic torque) on re-alignment of the vector of the magnetic dipole moment, and is equal to:

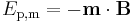$E_\mathrm{p,m} = -\mathbf{m}\cdot \mathbf{B}$ .

Electric circuits

The energy stored in an inductor (of inductance L) carrying current I is

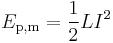$E_\mathrm{p,m} = \frac{1}{2}LI^2$ .

This second expression forms the basis for superconducting magnetic energy storage.

Electromagnetic energy

Examples of the interconversion of energy
Electromagnetic radiation is converted
into	by
Mechanical energy	Solar sail
Thermal energy	Solar collector
Electric energy	Solar cell
Electromagnetic radiation	Non-linear optics
Chemical energy	Photosynthesis
Nuclear energy	Mössbauer spectroscopy

Calculating work needed to create an electric or magnetic field in unit volume (say, in a capacitor or an inductor) results in the electric and magnetic fields energy densities:

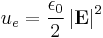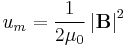$u_e=\frac{\epsilon_0}{2} \left| \mathbf{E} \right |^2 \,\!$ and $u_m=\frac{1}{2\mu_0} \left| \mathbf{B} \right |^2 \,\!$ , in SI units.

Electromagnetic radiation, such as microwaves, visible light or gamma rays, represents a flow of electromagnetic energy. Applying the above expressions to magnetic and electric components of electromagnetic field both the volumetric density and the flow of energy in EM field can be calculated. The resulting Poynting vector, which is expressed as

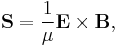
$\mathbf{S} = \frac{1}{\mu} \mathbf{E} \times \mathbf{B},$

in SI units, gives the density of the flow of energy and its direction.

The energy of electromagnetic radiation is quantized (has discrete energy levels). The energy of a photon is:

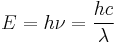$E = h\nu = \frac{hc}{\lambda}\,\!$ ,

so the spacing between energy levels is:

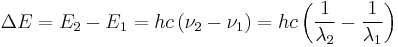$\Delta E = E_2 - E_1 = hc \left ( \nu_2 - \nu_1 \right ) = hc \left ( \frac{1}{\lambda_2} - \frac{1}{\lambda_1} \right ) \,\!$ ,

where h is the Planck constant, 6.6260693(11)×10⁻³⁴ Js,^[1] and ν is the frequency of the radiation. This quantity of electromagnetic energy is usually called a photon. The photons which make up visible light have energies of 270–520 yJ, equivalent to 160–310 kJ/mol, the strength of weaker chemical bonds.

Chemical energy

Main article: Chemical thermodynamics

Examples of the interconversion of energy
Chemical energy is converted
into	by
Mechanical energy	Muscle
Thermal energy	Fire
Electric energy	Fuel cell
Electromagnetic radiation	Glowworms
Chemical energy	Chemical reaction

Chemical energy is the energy due to associations of atoms in molecules and various other kinds of aggregates of matter. It may be defined as a work done by electric forces during re-arrangement of mutual positions of electric charges, electrons and protons, in the process of aggregation. So, basically it is electrostatic potential energy of electric charges. If the chemical energy of a system decreases during a chemical reaction, the difference is transferred to the surroundings in some form (often heat or light); on the other hand if the chemical energy of a system increases as a result of a chemical reaction - the difference then is supplied by the surroundings (usually again in form of heat or light). For example,

when two hydrogen atoms react to form a dihydrogen molecule, the chemical energy decreases by 724 zJ (the bond energy of the H–H bond);

when the electron is completely removed from a hydrogen atom, forming a hydrogen ion (in the gas phase), the chemical energy increases by 2.18 aJ (the ionization energy of hydrogen).

It is common to quote the changes in chemical energy for one mole of the substance in question: typical values for the change in molar chemical energy during a chemical reaction range from tens to hundreds of kilojoules per mole.

The chemical energy as defined above is also referred to by chemists as the internal energy, U: technically, this is measured by keeping the volume of the system constant. Most practical chemistry is performed at constant pressure and, if the volume changes during the reaction (e.g. a gas is given off), a correction must be applied to take account of the work done by or on the atmosphere to obtain the enthalpy, H, this correction is the work done by an expanding gas,

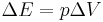$\Delta E = p \Delta V \,\!$ ,

so the enthalpy now reads;

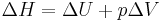$\Delta H = \Delta U %2B p \Delta V \,\!$ .

A second correction, for the change in entropy, S, must also be performed to determine whether a chemical reaction will take place or not, giving the Gibbs free energy, G. The correction is the energy required to create order from disorder,^[2]

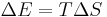$\Delta E = T \Delta S \,\!$ ,

so we have;

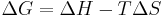$\Delta G = \Delta H - T \Delta S \,\!$ .

These corrections are sometimes negligible, but often not (especially in reactions involving gases).

Since the industrial revolution, the burning of coal, oil, natural gas or products derived from them has been a socially significant transformation of chemical energy into other forms of energy. the energy "consumption" (one should really speak of "energy transformation") of a society or country is often quoted in reference to the average energy released by the combustion of these fossil fuels:

1 tonne of coal equivalent (TCE) = 29.3076 GJ = 8,141 kilowatt hour

1 tonne of oil equivalent (TOE) = 41.868 GJ = 11,630 kilowatt hour

On the same basis, a tank-full of gasoline (45 litres, 12 gallons) is equivalent to about 1.6 GJ of chemical energy. Another chemically based unit of measurement for energy is the "tonne of TNT", taken as 4.184 GJ. Hence, burning a tonne of oil releases about ten times as much energy as the explosion of one tonne of TNT: fortunately, the energy is usually released in a slower, more controlled manner.

Simple examples of storage of chemical energy are batteries and food. When food is digested and metabolized (often with oxygen), chemical energy is released, which can in turn be transformed into heat, or by muscles into kinetic energy.

According to the Bohr theory of the atom, the chemical energy is characterized by the Rydberg constant. 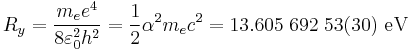$R_y= \frac{m_e e^4}{8 \varepsilon_0^2 h^2} = \frac{1}{2}\alpha^2 m_ec^2 = 13.605\;692\;53(30) \ \mathrm{eV}$ (see Rydberg constant for the meaning of the symbols).

Nuclear energy

Main article: Nuclear binding energy

Examples of the interconversion of energy
Nuclear binding energy is converted
into	by
Mechanical energy	Alpha radiation
Thermal energy	Sun
Electrical energy	Beta radiation
Electromagnetic radiation	Gamma radiation
Chemical energy	Radioactive decay
Nuclear energy	Nuclear isomerism

Nuclear potential energy, along with electric potential energy, provides the energy released from nuclear fission and nuclear fusion processes. The result of both these processes are nuclei in which the more-optimal size of the nucleus allows the nuclear force (which is opposed by the electromagnetic force) to bind nuclear particles more tightly together than before the reaction.

The Weak nuclear force (different from the strong force) provides the potential energy for certain kinds of radioactive decay, such as beta decay.

The energy released in nuclear processes is so large that the relativistic change in mass (after the energy has been removed) can be as much as several parts per thousand.

Nuclear particles (nucleons) like protons and neutrons are not destroyed (law of conservation of baryon number) in fission and fusion processes. A few lighter particles may be created or destroyed (example: beta minus and beta plus decay, or electron capture decay), but these minor processes are not important to the immediate energy release in fission and fusion. Rather, fission and fusion release energy when collections of baryons become more tightly bound, and it is the energy associated with a fraction of the mass of the nucleons (but not the whole particles) which appears as the heat and electromagnetic radiation generated by nuclear reactions. This heat and radiation retains the "missing" mass, but the mass is missing only because it escapes in the form of heat or light, which retain the mass and conduct it out of the system where it is not measured.

The energy from the Sun, also called solar energy, is an example of this form of energy conversion. In the Sun, the process of hydrogen fusion converts about 4 million metric tons of solar "matter" per second into light, which is radiated into space, but during this process, although protons change into neutrons, the number of total protons-plus-neutrons does not change. In this system, the radiated light itself (as a system) retains the "missing" mass, which represents 4 million tons per second of electromagnetic radiation, moving into space. Each of the helium nuclei which are formed in the process are less massive than the four protons from they were formed, but (to a good approximation), no particles are destroyed in the process of turning the Sun's nuclear potential energy into light. Instead, the four nucleons in a helium nucleus in the Sun have an average mass that is less than the protons which formed them, and this mass difference (4 million tons/second) is the mass that moves off as sunlight.

The nuclear binding energy formula, similar to that of the chemical energy, has been found^[3]

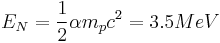
$E_N=\frac{1}{2}\alpha m_pc^2 =3.5 MeV$

where 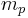$m_p$ is the mass of the proton

References

^ ^a ^b ^c Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Rev. Mod. Phys. 80: 633–730. Bibcode 2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633. http://physics.nist.gov/cuu/Constants/codata.pdf.
^ Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN 0-19-855148-7
^ J Fusion Energy (2011) 30 :377-381

Energy

Fundamental concepts	Energy · Power · Energetics · Laws of thermodynamics · Units of energy · Conversion of units of energy

Primary energy sources	Fossil fuel (Coal, Petroleum, Natural gas) · Mineral fuel (Natural uranium) · Solar · Wind · Bioenergy (Biomass) · Water (Hydroenergy, Marine energy) · Geothermal

Energy carriers	Fuel oil · Enthalpy (Heat) · Mechanical work · Electricity

Energy systems	Oil refinery · Fossil fuel power station (Coal-fired power plant, IGCC power plant, CHP plant) · Nuclear power (Nuclear power plant) · Solar power (Photovoltaic power plant, CSP plant) · Solar thermal energy (Solar power tower, Solar furnace) · Wind power (Wind farm, Offshore wind farm, Small-scale wind turbine, HAWP plant) · Hydropower (Hydropower plant, Wave farm, Tidal power station) · Biomass-fueled power plant · Geothermal power plant

Forms of energy

Contents

Mechanical energy

Mechanical work

Potential energy

Elastic potential energy

Kinetic energy

Surface energy

Sound energy

Gravitational potential energy

Thermal energy

Electric energy

Electrostatic energy

Electric energy

Magnetic energy

Electromagnetic energy

Chemical energy

Nuclear energy

References