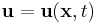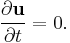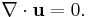Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid. The length of the flow velocity vector is the flow speed.

Contents

Definition

The flow velocity u of a fluid is a vector field

\mathbf{u}=\mathbf{u}(\mathbf{x},t)

which gives the velocity of an element of fluid at a position 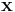\mathbf{x}\, and time t\, .

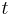The flow speed q is the length of the flow velocity vector[1]

q = || \mathbf{u} ||

and is a scalar field.

Uses

The flow velocity of a fluid effectively describes everything about the motion of a fluid. Many physical properties of a fluid can be expressed mathematically in terms of the flow velocity. Some common examples follow:

Steady flow

Main article: Steady flow

The flow of a fluid is said to be steady if 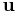\mathbf{u} does not vary with time. That is if

\frac{\partial \mathbf{u}}{\partial t}=0.

Incompressible flow

Main article: Incompressible flow

A fluid is incompressible if the divergence of 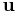\mathbf{u} is zero:

\nabla\cdot\mathbf{u}=0.

That is, if 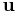\mathbf{u} is a solenoidal vector field.

Irrotational flow

Main article: Irrotational flow

A flow is irrotational if the curl of 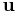\mathbf{u} is zero:

\nabla\times\mathbf{u}=0.

That is, if 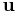\mathbf{u} is an irrotational vector field.

Vorticity

Main article: Vorticity

The vorticity, \omega, of a flow can be defined in terms of its flow velocity by

\omega=\nabla\times\mathbf{u}.

Thus in irrotational flow the vorticity is zero.

The velocity potential

Main article: Potential flow

If an irrotational flow occupies a simply-connected fluid region then there exists a scalar field \phi such that

\mathbf{u}=\nabla\mathbf{\phi}

The scalar field \phi is called the velocity potential for the flow. (See Irrotational vector field.)

Notes and references

  1. ^ Courant, R.; Friedrichs, K.O. (1977) (5th ed.), Springer, ISBN 0387902325 , p. 24