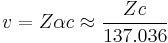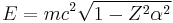Untriseptium
|
||||||
| Appearance | ||||||
|---|---|---|---|---|---|---|
| General properties | ||||||
| Name, symbol, number | untriseptium, Uts, 137 | |||||
| Element category | superactinides | |||||
| Group, period, block | n/a, 8, g | |||||
| Standard atomic weight | unknown | |||||
| Electron configuration | [Uuo] 5g17 8s2 (predicted) |
|||||
| Electrons per shell | 2, 8, 18, 32, 49, 18, 8, 2 (predicted) (Image) |
|||||
| Physical properties | ||||||
| Atomic properties | ||||||
Untriseptium ( /ˌuːntraɪˈsɛptiəm/), also known as eka-dubnium or element 137, is a hypothetical chemical element which has not been observed to occur naturally, nor has it yet been synthesised. Due to drip instabilities, it is not known if this element is physically possible. Its atomic number is 137 and symbol is Uts.
The name untriseptium is a temporary IUPAC systematic element name.
Contents |
Significance
Untriseptium is sometimes called feynmanium (symbol Fy) because Richard Feynman noted[1] that a simplistic interpretation of the relativistic Dirac equation runs into problems with electron orbitals at Z > 1/α = 137, suggesting that neutral atoms cannot exist beyond untriseptium, and that a periodic table of elements based on electron orbitals therefore breaks down at this point. However, a more rigorous analysis calculates the limit to be Z ≈ 173.[2]
Bohr model breakdown
The Bohr model exhibits difficulty for atoms with atomic number greater than 137, for the speed of an electron in a 1s electron orbital, v, is given by
where Z is the atomic number, and α is the fine structure constant, a measure of the strength of electromagnetic interactions.[3] Under this approximation, any element with an atomic number of greater than 137 would require 1s electrons to be traveling faster than c, the speed of light. Hence the non-relativistic Bohr model is clearly inaccurate when applied to such an element.
The Dirac equation
The relativistic Dirac equation also has problems for Z > 137, for the ground state energy is
where m is the rest mass of the electron. For Z > 137, the wave function of the Dirac ground state is oscillatory, rather than bound, and there is no gap between the positive and negative energy spectra, as in the Klein paradox.[4]
More accurate calculations including the effects of the finite size of the nucleus indicate that the binding energy first exceeds 2mc2 for Z > Zcr ≈ 173. For Z > Zcr, if the innermost orbital is not filled, the electric field of the nucleus will pull an electron out of the vacuum, resulting in the spontaneous emission of a positron.[5]
More complete analysis involving relativity shows that the contradiction this particle poses may actually occur in the hypothetical element untriennium (Z = 139; see unsolved problems in chemistry).
See also
References
- ^ Elert, G.. "Atomic Models". The Physics Hypertextbook. http://physics.info/atomic-models/. Retrieved 2009-10-09.
- ^ See Extended periodic table.
- ^ See for example Eisberg, R.; Resnick, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles. Wiley.
- ^ Bjorken, J. D.; Drell, S. D. (1964). Relativistic Quantum Mechanics. McGraw-Hill.
- ^ Greiner, W.; Schramm, S. (2008). American Journal of Physics. 76. pp. 509., and references therein.
| H | He | |||||||||||||||||||||||||||||||||||||||||
| Li | Be | B | C | N | O | F | Ne | |||||||||||||||||||||||||||||||||||
| Na | Mg | Al | Si | P | S | Cl | Ar | |||||||||||||||||||||||||||||||||||
| K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr | |||||||||||||||||||||||||
| Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe | |||||||||||||||||||||||||
| Cs | Ba | La | Ce | Pr | Nd | Pm | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn | |||||||||||
| Fr | Ra | Ac | Th | Pa | U | Np | Pu | Am | Cm | Bk | Cf | Es | Fm | Md | No | Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Uut | Uuq | Uup | Uuh | Uus | Uuo | |||||||||||
| Uue | Ubn | Ute | Uqn | Uqu | Uqb | Uqt | Uqq | Uqp | Uqh | Uqs | Uqo | Uqe | Upn | Upu | Upb | Upt | Upq | Upp | Uph | Ups | Upo | Upe | Uhn | Uhu | Uhb | Uht | Uhq | Uhp | Uhh | Uhs | Uho | |||||||||||
| Uhe | Usn | |||||||||||||||||||||||||||||||||||||||||
| Ubu | Ubb | Ubt | Ubq | Ubp | Ubh | Ubs | Ubo | Ube | Utn | Utu | Utb | Utt | Utq | Utp | Uth | Uts | Uto | |||||||||||||||||||||||||
| Usu | Usb | Ust | ||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||