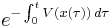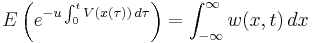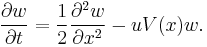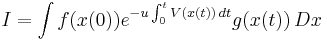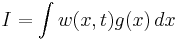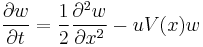Feynman–Kac formula
The Feynman–Kac formula, named after Richard Feynman and Mark Kac, establishes a link between parabolic partial differential equations (PDEs) and stochastic processes. It offers a method of solving certain PDEs by simulating random paths of a stochastic process. Conversely, an important class of expectations of random processes can be computed by deterministic methods. Consider the PDE,
defined for all real  and
and  in the interval
in the interval ![[0, T]](/2012-wikipedia_en_all_nopic_01_2012/I/b74093923941d33ee19becc5f4b48b25.png) , subject to the terminal condition
, subject to the terminal condition
where 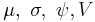 are known functions,
are known functions, 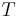 is a parameter and
is a parameter and 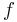 is the unknown. Then the Feynman–Kac formula tells us that the solution can be written as an expectation:
is the unknown. Then the Feynman–Kac formula tells us that the solution can be written as an expectation:
where 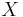 is an Itō process driven by the equation
is an Itō process driven by the equation
with 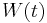 is a Wiener process (also called Brownian motion) and the initial condition for
is a Wiener process (also called Brownian motion) and the initial condition for 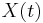 is
is 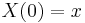 . This expectation can then be approximated using Monte Carlo or quasi-Monte Carlo methods.
. This expectation can then be approximated using Monte Carlo or quasi-Monte Carlo methods.
Contents |
Proof
NOTE: The proof presented below is essentially that of,[1] albeit with more detail. Let  be the solution to above PDE. Applying Itō's lemma to the process
be the solution to above PDE. Applying Itō's lemma to the process 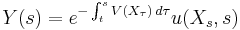 one gets
one gets
Since 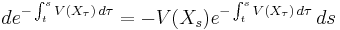 , the third term is
, the third term is 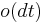 and can be dropped. Applying Itō's lemma once again to
and can be dropped. Applying Itō's lemma once again to 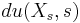 , it follows that
, it follows that
The first term contains, in parentheses, the above PDE and is therefore zero. What remains is
Integrating this equation from  to
to  , one concludes that
, one concludes that
Upon taking expectations, conditioned on 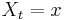 , and observing that the right side is an Itō integral, which has expectation zero, it follows that
, and observing that the right side is an Itō integral, which has expectation zero, it follows that ![E[Y(T)| X_t=x] = E[Y(t)| X_t=x] = u(x,t)](/2012-wikipedia_en_all_nopic_01_2012/I/20e68f77b0ff709c113231958de610c2.png) . The desired result is obtained by observing that
. The desired result is obtained by observing that
Remarks
When originally published by Kac in 1949,[2] the Feynman–Kac formula was presented as a formula for determining the distribution of certain Wiener functionals. Suppose we wish to find the expected value of the function
in the case where 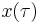 is some realization of a diffusion process starting at
is some realization of a diffusion process starting at 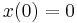 . The Feynman–Kac formula says that this expectation is equivalent to the integral of a solution to a diffusion equation. Specifically, under the conditions that
. The Feynman–Kac formula says that this expectation is equivalent to the integral of a solution to a diffusion equation. Specifically, under the conditions that 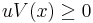 ,
,
where 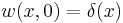 and
and
The Feynman–Kac formula can also be interpreted as a method for evaluating functional integrals of a certain form. If
where the integral is taken over all random walks, then
where 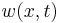 is a solution to the parabolic partial differential equation
is a solution to the parabolic partial differential equation
with initial condition 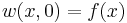 .
.
See also
- Itō's lemma
- Kunita–Watanabe theorem
- Girsanov theorem
- Kolmogorov forward equation (also known as Fokker–Planck equation)
References
- Simon, Barry (1979). Functional Integration and Quantum Physics. Academic Press.
- ^ http://www.math.nyu.edu/faculty/kohn/pde_finance.html
- ^ Kac, Mark (1949). "On Distributions of Certain Wiener Functionals". Transactions of the American Mathematical Society 65 (1): 1–13. doi:10.2307/1990512. JSTOR 1990512.
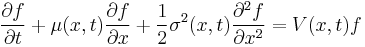
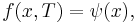
![\ f(x,t) = E[ e^{- \int_t^T V(X_\tau)\, d\tau}\psi(X_T) | X_t=x ]](/2012-wikipedia_en_all_nopic_01_2012/I/0680f182186db9e2f17b3d2c5b99c8db.png)
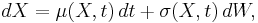
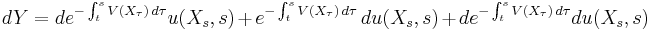
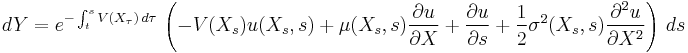
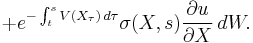
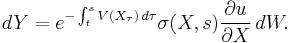
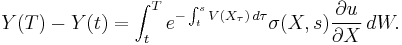
![E[Y(T)| X_t=x] = E[e^{- \int_t^T V(X_\tau)\, d\tau} u(X_T,T)| X_t=x] = E[e^{- \int_t^T V(X_\tau)\, d\tau} \psi(X_T))| X_t=x]](/2012-wikipedia_en_all_nopic_01_2012/I/7fda6f528d9bda4d214c4b540af7b0c4.png)