Feynman slash notation

In the study of Dirac fields in quantum field theory, Richard Feynman invented the convenient Feynman slash notation (less commonly known as the Dirac slash notation[1]). If A is a covariant vector (i.e., a 1-form),

A\!\!\!/\ \stackrel{\mathrm{def}}{=}\ \gamma^\mu A_\mu

using the Einstein summation notation where γ are the gamma matrices.

Contents

Identities

Using the anticommutators of the gamma matrices, one can show that for any a_\mu and b_\mu,

a\!\!\!/a\!\!\!/=a^\mu a_\mu=a^2
a\!\!\!/b\!\!\!/%2Bb\!\!\!/a\!\!\!/ = 2 a \cdot b \,.

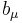In particular,

\partial\!\!\!/^2=\partial^2.

Further identities can be read off directly from the gamma matrix identities by replacing the metric tensor with inner products. For example,

\operatorname{tr}(a\!\!\!/b\!\!\!/) = 4 a \cdot b
\operatorname{tr}(a\!\!\!/b\!\!\!/c\!\!\!/d\!\!\!/) = 4 \left[(a\cdot b)(c \cdot d) - (a \cdot c)(b \cdot d) %2B (a \cdot d)(b \cdot c) \right]
\operatorname{tr}(\gamma_5 a\!\!\!/b\!\!\!/c\!\!\!/d\!\!\!/) = 4 i \epsilon_{\mu \nu \lambda \sigma} a^\mu b^\nu c^\lambda d^\sigma
\gamma_\mu a\!\!\!/ \gamma^\mu = -2 a\!\!\!/ .
\gamma_\mu a\!\!\!/ b\!\!\!/ \gamma^\mu = 4 a \cdot b \,
\gamma_\mu a\!\!\!/ b\!\!\!/ c\!\!\!/ \gamma^\mu = -2 c\!\!\!/ b\!\!\!/ a\!\!\!/ \,
where
\epsilon_{\mu \nu \lambda \sigma} \, is the Levi-Civita symbol.

With four-momentum

Often, when using the Dirac equation and solving for cross sections, one finds the slash notation used on four-momentum:

using the Dirac basis for the 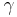\gamma\,'s,

\gamma^0 = \begin{pmatrix} I & 0 \\ 0 & -I \end{pmatrix},\quad \gamma^i = \begin{pmatrix} 0 & \sigma^i \\ -\sigma^i & 0 \end{pmatrix} \,

as well as the definition of four momentum

p_{\mu} = \left(E, -p_x, -p_y, -p_z \right) \,

We see explicitly that

\begin{align} p\!\!/ &= \gamma^\mu p_\mu = \gamma^0 p_0 %2B \gamma^i p_i \\ &= \begin{bmatrix} p_0 & 0 \\ 0 & -p_0 \end{bmatrix} %2B \begin{bmatrix} 0 & \sigma^i p_i \\ - \sigma^i p_i & 0 \end{bmatrix} \\ &= \begin{bmatrix} E & - \sigma \cdot \vec p \\ \sigma \cdot \vec p & -E \end{bmatrix} \end{align}

See also

References

  1. ^ Steven Weinberg (1964), The quantum theory of fields, Volume 2, Cambridge University Press, 1995, pp. 358, ISBN 0521550017, http://books.google.com/books?id=3ws6RJzqisQC&lpg=PA358&dq=%22Dirac%20Slash%22&pg=PA358#v=onepage&q&f=false 
  • Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.