Feedback vertex set

In the mathematical discipline of graph theory, a feedback vertex set of a graph is a set of vertices whose removal leaves a graph without cycles. In other words, each feedback vertex set contains at least one vertex of any cycle in the graph. The feedback vertex set problem is an NP-complete problem in computational complexity theory. It was among the first problems shown to be NP-complete. It has wide applications in operating system, database system, genome assembly, and VLSI chip design.

Contents

Definition

The decision problem is as follows:

INSTANCE: An (undirected or directed) graph 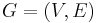G = (V, E) and a positive integer k.
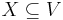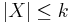QUESTION: Is there a subset X \subseteq V with |X| \leq k such that G with the vertices from X deleted is cycle-free?

The graph G[V \setminus X] that remains after removing X from G is an induced forest (resp. an induced directed acyclic graph in the case of directed graphs). Thus, finding a minimum feedback vertex set in a graph is equivalent to finding a maximum induced forest (resp. maximum induced directed acyclic graph in the case of directed graphs).

NP-hardness

Karp (1972) showed that the feedback vertex set problem for directed graphs is NP-complete. The problem remains NP-complete on directed graphs with maximum in-degree and out-degree two, and on directed planar graphs with maximum in-degree and out-degree three.[1] Karp's reduction also implies the NP-completeness of the feedback vertex set problem on undirected graphs, where the problem stays NP-hard on graphs of maximum degree four.

Note that the problem of deleting edges to make the graph cycle-free is equivalent to finding a minimum spanning tree, which can be done in polynomial time. In contrast, the problem of deleting edges from a directed graph to make it acyclic, the feedback arc set problem, is NP-complete, see Karp (1972).

Exact algorithms

The corresponding NP optimization problem of finding the size of a minimum feedback vertex set can be solved in time O(1.7347n), where n is the number of vertices in the graph.[2] This algorithm actually computes a maximum induced forest, and when such a forest is obtained, its complement is a minimum feedback vertex set. The number of minimal feedback vertex sets in a graph is bounded by O(1.8638n).[3] The directed feedback vertex set problem can still be solved in time O*(1.9977n), where n is the number of vertices in the given directed graph.[4] The parameterized versions of the directed and undirected problems are both fixed-parameter tractable.[5]

Approximation

The problem is APX-complete, which directly follows from the APX-completeness of the vertex cover problem,[6] and the existence of an approximation preserving L-reduction from the vertex cover problem to it.[7] The best known approximation on undirected graphs is by a factor of two.[8]

Bounds

According to the Erdős–Pósa theorem, the size of a minimum feedback vertex set is within a logarithmic factor of the maximum number of vertex-disjoint cycles in the given graph.

Applications

In operating systems, feedback vertex sets play a prominent role in the study of deadlock recovery. In the wait-for graph of an operating system, each directed cycle corresponds to a deadlock situation. In order to resolve all deadlocks, some blocked processes have to be aborted. A minimum feedback vertex set in this graph corresponds to a minimum number of processes that one needs to abort (Silberschatz & Galvin 2008).

Furthermore, the feedback vertex set problem has applications in VLSI chip design (cf. Festa, Pardalos & Resende (2000)) and genome assembly.

Notes

  1. ^ unpublished results due to Garey and Johnson, cf. Garey & Johnson (1979): GT7
  2. ^ Fomin & Villanger (2010)
  3. ^ Fomin et al. (2008)
  4. ^ Razgon (2007)
  5. ^ Chen et al. (2008)
  6. ^ Dinur & Safra 2005
  7. ^ Karp (1972)
  8. ^ Becker & Geiger (1996)

References

Research articles

  • Ann Becker, Reuven Bar-Yehuda, Dan Geiger: Randomized Algorithms for the Loop Cutset Problem. J. Artif. Intell. Res. (JAIR) 12: 219-234 (2000)
  • Becker, Ann; Geiger, Dan (1996), "Optimization of Pearl's Method of Conditioning and Greedy-Like Approximation Algorithms for the Vertex Feedback Set Problem.", Artif. Intell. 83 (1): 167–188, doi:10.1016/0004-3702(95)00004-6 
  • Jianer Chen, Fedor V. Fomin, Yang Liu, Songjian Lu, Yngve Villanger: Improved algorithms for feedback vertex set problems. J. Comput. Syst. Sci. 74(7): 1188-1198 (2008)
  • Jianer Chen, Yang Liu, Songjian Lu, Barry O'Sullivan, Igor Razgon: A fixed-parameter algorithm for the directed feedback vertex set problem. J. ACM 55(5): (2008)
  • Fomin, Fedor V.; Gaspers, Serge; Pyatkin, Artem; Razgon, Igor (2008), "On the Minimum Feedback Vertex Set Problem: Exact and Enumeration Algorithms.", Algorithmica 52 (2): 293–307, doi:10.1007/s00453-007-9152-0 
  • Fomin, Fedor V.; Villanger, Yngve (2010), "Finding Induced Subgraphs via Minimal Triangulations.", Proc. of STACS 2010, pp. 383–394, doi:10.4230/LIPIcs.STACS.2010.2470 
  • I. Razgon : Computing Minimum Directed Feedback Vertex Set in O*(1.9977n). In: Giuseppe F. Italiano, Eugenio Moggi, Luigi Laura (Eds.), Proceedings of the 10th Italian Conference on Theoretical Computer Science 2007, World Scientific, pp. 70–81 (author's version (pdf), preliminary full version (pdf)).

Textbooks and survey articles