Feed-Drum
The Feed-Drum [1] is an imperial bass drum with a system of electronic conditioning of the skin conceived by composer Michelangelo Lupone and produced at CRM - Centro Ricerche Musicali, Rome. Through the principle of feed-back, the signal produced by the excitation of the skin was returned to the skin itself in the form of acoustic pressure. The result was the infinite prolongation of the sound. The system controls the damping of the movement of the skin, and therefore the decay rate of the sound, and permits isolation of high frequency modes by the combined action of nodes present on the skin and the amount of feed-back input energy.[2] The design on the skin surface is a simplified map of the oscillatory modes based on the Bessel functions. The map was limited to 13 diameters and 8 nodal circles, the latter divided into even semicircles (to the left) and odd semicircles (to the right).[3]
Contents |
Experimental Work
Although the skin of an imperial bass drum allows the excitation of a considerable number of high-frequency modes, their duration in time is not normally appreciable by the listener, apart from the timbric contribution to the attack phase of the sound. The possible variations of the mode of emission, adequate for a sufficient acoustic response of the resonator (shell), are limited and with scarce modulability. The basic frequency, obtained by the tension of the skins, upper and lower, each bound to the edges with 16 mechanical tie rods, is influenced by the non-homogeneous distribution of the tensioning forces which contributes to render complex the spectrum of the real modes.[4]
Experiments were made at the Centro Ricerche Musicali - CRM in Rome [5][6] with the aim of achieving the following objectives:
1. variation of the basic frequency through the application of nodal constraints to the skin,
2. identification of timbres on the basis of type, mode and point of excitation,
3. sound modulation through glissandos, vibratos, portamento and rhythmic micro-articulation,
4. continuous and/or step variations of the dynamics, on the basis of the type of damping applied to the skin.
The characteristics of the traditional bass drum obviously do not permit the achievement of a range of acoustic results relevant to the proposed objectives. In order to explore the timbre richness of the attack phase and to isolate the vibrational modes, a system of electronic conditioning of the skin was created. Through the principle of feed-back, the signal produced by the excitation of the skin was returned to the skin itself in the form of acoustic pressure. The result was the infinite prolongation of the sound. The system controls the damping of the movement of the skin, and therefore the decay rate of the sound, and permits the isolation of high frequency modes by the combined action of the nodes present on the skin and of the amount of feed-back input energy.[7]
The stability of the signal obtained with this conditioning system made it possible to experiment and design on the skin surface a preliminary simplified map of the oscillatory modes based on the Bessel’s functions. The map was limited to 13 diameters and 8 nodal circles, the latter divided into even semicircles (to the left) and odd semicircles (to the right). Electronic conditioning of the instrument left the topology and primary acoustic features unaltered, but increased the scope of the vibrational criteria and control. This was used so that it was possible to distinguish the different pitches of various modes, to obtain the emission of long notes which could be modulated as those emitted by a stretched string and to adapt the acoustic energy independently of the emitted frequencies.[8]
In order to maintain agility of execution and an adequate reproducibility of the phenomena, the first classification of sounds and performance techniques was limited to the use of fingers, hands and arms (Fig. 4). During the composition of Gran Cassa by Michelangelo Lupone, experiments were also made with objects of different shapes and dimensions occupying wider or multiple nodal sections; this enabled to increase further the sound possibilities, but the complexity of the vibrational phenomena involved an analysis also of the mechanical parts of the instrument in order to comprehend and reduce the dispersions as well as the non-linear contribution introduced by the vibrations of the structural materials and their combinations.[9]
Given these complications, it was decided to plan and realize a new instrument, the Feed-drum (Fig. 5), for the purpose of not only extending the acoustic possibilities, but also of permitting the ergonomic use of new executive techniques. In particular, the vibrational attitude was transformed by eliminating the lower skin, a decision which simplified the tuning of the instrument’s basic frequency (30 Hz) and reduced the excitation rise time in the upper modes. A synthetic membrane was applied with isotropic characteristics and high flexibility on which the previously described map was drawn, with colors that made the areas of performance more visible. The shell and the tensioning hoop were realized in steel and aluminium; in particular, the tensioning hoop was made stiffer while the height was reduced and the adhesion surface increased. The suspension system was realized in such a way as to separate the Feed-drum completely from the supporting structure on the ground; all the mechanical parts, which were in contact with one another, were separated by an intermediate layer of antivibrational material.[10]
Theory of Operation
The behaviour of the Feed-drum is extremely complex and many of its aspects still have to be clarified. We will attempt to illustrate here the known elements, those conjectural and those remaining to be defined. The oscillation modes of a circular non-rigid membrane, pegged down and stretched along its rim, are known from literature. In a conservative model (that is, without dissipations and acoustic irradiations and therefore “in vacuum” ), the oscillation modes of a membrane of radius a have the form in cylindrical coordinates
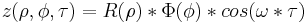 (1)
(1)
where: 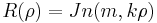 and
and 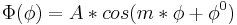
and where 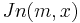 are Bessel functions of the first kind and of an order
are Bessel functions of the first kind and of an order 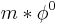 is an arbitrary phase dependent on the initial conditions (there cannot be any privileged directions, since the problem applies to a circular symmetry).
is an arbitrary phase dependent on the initial conditions (there cannot be any privileged directions, since the problem applies to a circular symmetry).
Owing to the constraint on the rim, 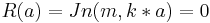 , where
, where  is the radius of the membrane; this allows calculating k (wave number) which is discrete and dependent on two indices (m,n):
is the radius of the membrane; this allows calculating k (wave number) which is discrete and dependent on two indices (m,n): 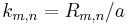 , where
, where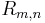 is the nth root of the Bessel function of order
is the nth root of the Bessel function of order 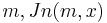 .
.
Hence (1) becomes 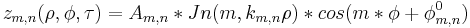 .
.
Determination of the wave number is therefore possible by determining the roots of the Bessel function of the first kind. Once the roots and wave numbers are determined, the angular frequencies peculiar to the modes are given by: 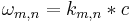 where c is the velocity propagation of transverse waves in the membrane,
where c is the velocity propagation of transverse waves in the membrane, 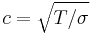 where
where  is the stretching force of the rim and
is the stretching force of the rim and  is the surface density of the membrane. However,
is the surface density of the membrane. However,  can easily be estimated on the basis of the frequency
can easily be estimated on the basis of the frequency 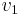 of mode
of mode 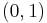 , the lowest of all (basic frequency), taking into account that
, the lowest of all (basic frequency), taking into account that 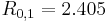 :
:
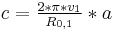
For the Feed-Drum, 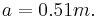 and
and 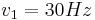 , and therefore
, and therefore 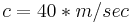 .
.
Irrespective of the order of the Bessel functions, the root base tends to  for
for 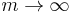 [2]; in addition, Bessel functions of different order do not have coincident roots (an important consideration for the purpose of the Feed-drum). The exact calculation of the roots can only be realized numerically, a task which is not particularly difficult given the oscillatory character (even if not periodical) of Bessel functions. In fact, the roots of these functions are each comprised between a maximum and a minimum or vice versa.
[2]; in addition, Bessel functions of different order do not have coincident roots (an important consideration for the purpose of the Feed-drum). The exact calculation of the roots can only be realized numerically, a task which is not particularly difficult given the oscillatory character (even if not periodical) of Bessel functions. In fact, the roots of these functions are each comprised between a maximum and a minimum or vice versa.
Calculations of the frequencies for the modes up to 5 octaves above the “basic frequency” (960 Hz for the Feed-drum) gives the following distributions of frequencies and modal density:
The index  is responsible for the creation of nodal diameters, the index
is responsible for the creation of nodal diameters, the index  for that of nodal circles. In general, the pattern of the modes is simply correlated to the indices, as can be seen from the diagrams given below.
for that of nodal circles. In general, the pattern of the modes is simply correlated to the indices, as can be seen from the diagrams given below.
Conditioning System and Implementation
Excitation of the membrane is via a loudspeaker (Ø = 45 cm.) and a 11 cm-long wave guide (designed to convey maximum acoustic pressure between the center and 1/3 of the radius); that is, fairly short as far as the form factor is concerned. It proved fairly easy to obtain, in addition to the 30 Hz basic frequency, the 68.9 Hz frequency corresponding to the mode (0,2). It was on the contrary impossible to obtain the frequency of 47.8 Hz corresponding to the mode (1,1). At these frequencies, the behavior of the air excited by the loudspeaker can presumably be schematized with a piston motion, which exercises an almost uniform pressure on the membrane. A uniform excitation is poorly compatible with the modal form (1,1). The loudspeaker was driven by an electric power signal, generated by a feed-back system that sampled the signal issued by a piezoceramic sensor placed on the rim and detecting deflection of the membrane. In this way a “multimodal” oscillator was obtained generating a feed-back on a resonant element, the membrane. The loop gain was controllable by a pedal.[11]
Intonation of the Upper Modes
Intonation is through the combined action of the negative feed-back gain and of the pressure on one or two points of a nodal line. The effect of the pressure can be schematized in a first approximation as dual: on one hand the introduction of a constraint on the pressure points, on the other a shift of the “work point” of the membrane around a slightly higher tension, and therefore an increase of the transverse wave velocity  . Consequently, all the frequencies move upwards. It is a matter of a shift mechanism, a “pitch-shift”, in the sense that the frequencies of the modes are all multiplied by a common factor, therefore leaving unchanged their relationships. In point of fact this effect has been encountered in practice and is utilized for obtaining the vibrato. The term “pitch-shift” is however improper in this case, since the spectrum of the partial tones of the membrane is not harmonic and as a result a pitch is not definable.
. Consequently, all the frequencies move upwards. It is a matter of a shift mechanism, a “pitch-shift”, in the sense that the frequencies of the modes are all multiplied by a common factor, therefore leaving unchanged their relationships. In point of fact this effect has been encountered in practice and is utilized for obtaining the vibrato. The term “pitch-shift” is however improper in this case, since the spectrum of the partial tones of the membrane is not harmonic and as a result a pitch is not definable.
The apposition of constraint points (z = 0) has the effect, as a rule, of inhibiting every mode which has no set of nodal lines passing through all the aforesaid points, not even with an opportune choice of 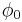 .
.
For example, pressing the center of the membrane makes all the modes with 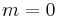 becoming impracticable, since this point is invariably an antinode for these modes. Pressure on any other point of the membrane (speaking theoretically) makes all the modes with
becoming impracticable, since this point is invariably an antinode for these modes. Pressure on any other point of the membrane (speaking theoretically) makes all the modes with 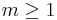 practicable, since it will always be possible to have a nodal diameter passing through that point. In practice, since the constraint is not perfect, preference will be given to the mode which possesses both a nodal diameter and a nodal circle passing through that point. The consequence of the fact that the functions of Bessel have no coincident roots is that the modes of different m order cannot have coincident nodal circles. Even modes with the same m and different n obviously cannot have coincident nodal circles. Two different modes can, on the other hand, have coincident nodal diameters if the ratio of their indices m is an integer number. A single pressure point different from the centre identifies therefore a mode only having a diameter and a circle passing through that point. The points which “discriminate” better the frequency modes are, however, those near the centre, because the nodal circles become densely-packed towards the perimeter and a single point therefore tends to have many of them very near to it. Consequently, it is the first nodal circle, the innermost one, which best discriminates the modes, as is also shown by a variance analysis.
practicable, since it will always be possible to have a nodal diameter passing through that point. In practice, since the constraint is not perfect, preference will be given to the mode which possesses both a nodal diameter and a nodal circle passing through that point. The consequence of the fact that the functions of Bessel have no coincident roots is that the modes of different m order cannot have coincident nodal circles. Even modes with the same m and different n obviously cannot have coincident nodal circles. Two different modes can, on the other hand, have coincident nodal diameters if the ratio of their indices m is an integer number. A single pressure point different from the centre identifies therefore a mode only having a diameter and a circle passing through that point. The points which “discriminate” better the frequency modes are, however, those near the centre, because the nodal circles become densely-packed towards the perimeter and a single point therefore tends to have many of them very near to it. Consequently, it is the first nodal circle, the innermost one, which best discriminates the modes, as is also shown by a variance analysis.
In theory, pressure on any two points of the membrane could create constraints incompatible with any mode.
However, all these considerations are better limited to modes of relatively low order. In fact it can be presumed that the approximation of the non-rigid membrane results less valid with the increase of the mode order, since the node base tends to become comparable with the thickness of the membrane itself. There are also other considerations. The classic equation of the membrane generally used for obtaining the modes is entirely conservative and does not take into account either dissipation due to internal friction or irradiation. The latter both being mechanisms that dampen the partials, causing their decay in the absence of an exciting force. A symbolical solution of the equation corresponding to the vibro-acoustic movement described is definitely impossible, even if greatly simplifying hypotheses are adopted. It is certainly possible to solve it with numerical methods (such as FEM, BEM, etc.) but even in this case, if acoustic-elastic coupling and internal dissipations of the membrane are to be taken into account, the problem still remains extremely delicate and the results should be subjected to thorough experimental verification. However, even in the absence of a solution, it is possible to note that decay of the partials is in any case connected with the merit factor (Q) of their resonance and provokes a widening of the spectral line, always more marked the more the relative mode is damped. The internal frictions are proportional to the velocity of variation of the local curvature, which increases with the frequency. It can therefore be presumed that, similarly to stretched strings, damping of the modes increases with their frequency. Consequently, in the upper spectral areas, where the modes are close together and massed (see Figs. 9 & 10), the transfer function of the membrane is more continuous than discrete, with moderate peaks on the modal frequencies. In these areas the modes which can be excited are less precisely definable and depend on the loop gain and on the frequency characteristics of the negative feedback electronic circuit. Conversely, the passage from one mode to another of adjacent frequency has little influence on the resultant frequency. Construction of a future improved map for excitation of modes must therefore foresee a judicious choice of the pairs of points which offer the most significant discrimination between modes. In addition, the modal frequencies should be verified experimentally, since it can be presumed that the frequencies of some modes deviate from their nominal values owing to the presence of the actuator with relative wave guide which has a beam width equal to 1/3 of the membrane diameter. The measurement of these deviations cannot be determined reliably with theoretical considerations, since the overall model is too complex and can only be solved (as already shown) with numerical methods.
Further Development
The trials carried out to date with composers and percussionists stimulated suggestions for extending the control criteria, the use of special strikers of various forms and dimensions, and the application of independent hand techniques.[12] Subsequent developments will principally concern ergonomic aspects, with the compilation of more precise nodal maps, of simpler and immediate use. In addition, improvements are quite conceivable in the electronic conditioning system and in its operation for the purpose of improving controllability of the emission of high overtones.[13]
See also
References
- ^ GRAME Rencontre Musicales Pluridisciplinaries 2006 Retrieved on August 18, 2009.
- ^ Universidad Complutense de Madrid
- ^ Max Planck Institut - Informatik
- ^ Exibart
- ^ Gran Cassa and the Adaptive Instrument Feed-Drum - Computer Music Modeling and Retrieval - Seno, Lorenzo - Lupone, Michelangelo - Spinger Verlag 2006 - ISBN 3-540-34027-0
- ^ CRM - Centro Ricerche Musicali
- ^ Springer Berlin Heidelberg
- ^ INIST/CNRS
- ^ LMA CNRS MRS France
- ^ Conservatory of Music Alfredo Casella L'Aquila Retrieved on August 21, 2009
- ^ Corriere della Sera
- ^ ItaliaFestival
- ^ YouTube