Fano variety

In algebraic geometry, a Fano variety, introduced by (Fano 1934, 1942), is a non-singular complete variety whose anticanonical bundle is ample.

Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces.

Contents

The example of projective hypersurfaces

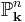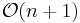The fundamental example of Fano varieties are the projective spaces: the anticanonical line bundle of \mathbb P_{\mathbf k}^n is \mathcal O(n%2B1), which is very ample (its curvature is n+1 times the Fubini–Study symplectic form).

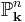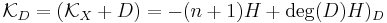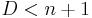Let D be a smooth Weil divisor in \mathbb P_{\mathbf k}^n, from the adjunction formula, we infer \mathcal K_D = (\mathcal K_X %2B D) = -(n%2B1) H %2B \mathrm{deg}(D) H )_D, where H is the class of the hyperplane. The hypersurface D is therefore Fano if and only if D < n%2B1.

Some properties

The existence of an ample line bundle on X is equivalent to X being a projective variety, so this is the case for Fano varieties. The Kodaira vanishing theorem implies that the higher cohomology groups 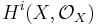H^i(X, \mathcal O_X) of the structure sheaf vanish for 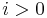i > 0. In particular, the first Chern class induces an isomorphism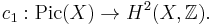 c_1�: \mathrm{Pic}(X) \to H^2(X,\mathbb Z).

A Fano variety is simply connected and is uniruled, in particular it has Kodaira dimension −∞.

Classification in small dimensions

Fano varieties in dimensions 1 are isomorphic to the projective line.

In dimension 2 they are del Pezzo surfaces and are isomorphic to either 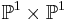\mathbb{P}^1 \times \mathbb{P}^1 or to the projective plane blown up in at most 8 general points, and in particular are again all rational.

In dimension 3 there are non-rational examples. Iskovskih () classified the Fano 3-folds with second Betti number 1 into 17 classes, and Mori & Mukai (1981) classified the ones with second Betti number at least 2, finding 88 deformation classes.

References