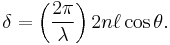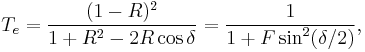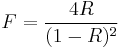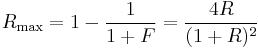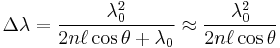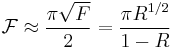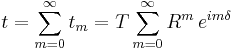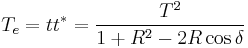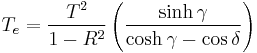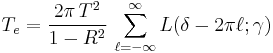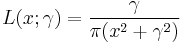Fabry–Pérot interferometer
In optics, a Fabry–Pérot interferometer or etalon is typically made of a transparent plate with two reflecting surfaces, or two parallel highly reflecting mirrors. (Technically the former is an etalon and the latter is an interferometer, but the terminology is often used inconsistently.) Its transmission spectrum as a function of wavelength exhibits peaks of large transmission corresponding to resonances of the etalon. It is named after Charles Fabry and Alfred Perot.[1] "Etalon" is from the French étalon, meaning "measuring gauge" or "standard".[2]
The resonance effect of the Fabry–Pérot interferometer is identical to that used in a dichroic filter. That is, dichroic filters are very thin sequential arrays of Fabry–Pérot interferometers, and are therefore characterised and designed using the same mathematics.
Etalons are widely used in telecommunications, lasers and spectroscopy to control and measure the wavelengths of light. Recent advances in fabrication technique allow the creation of very precise tunable Fabry–Pérot interferometers.
Contents |
Theory
The varying transmission function of an etalon is caused by interference between the multiple reflections of light between the two reflecting surfaces. Constructive interference occurs if the transmitted beams are in phase, and this corresponds to a high-transmission peak of the etalon. If the transmitted beams are out-of-phase, destructive interference occurs and this corresponds to a transmission minimum. Whether the multiply reflected beams are in phase or not depends on the wavelength (λ) of the light (in vacuum), the angle the light travels through the etalon (θ), the thickness of the etalon (ℓ) and the refractive index of the material between the reflecting surfaces (n).
The phase difference between each succeeding reflection is given by δ:[3]
If both surfaces have a reflectance R, the transmittance function of the etalon is given by
where
is the coefficient of finesse.
Maximum transmission (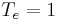 ) occurs when the optical path length difference (
) occurs when the optical path length difference (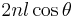 ) between each transmitted beam is an integer multiple of the wavelength. In the absence of absorption, the reflectance of the etalon Re is the complement of the transmittance, such that
) between each transmitted beam is an integer multiple of the wavelength. In the absence of absorption, the reflectance of the etalon Re is the complement of the transmittance, such that 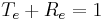 . The maximum reflectivity is given by:
. The maximum reflectivity is given by:
and this occurs when the path-length difference is equal to half an odd multiple of the wavelength.
The wavelength separation between adjacent transmission peaks is called the free spectral range (FSR) of the etalon, Δλ, and is given by:
where λ0 is the central wavelength of the nearest transmission peak. The FSR is related to the full-width half-maximum, δλ, of any one transmission band by a quantity known as the finesse:
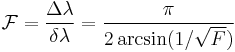 .
.
This is commonly approximated (for R > 0.5) by
Etalons with high finesse show sharper transmission peaks with lower minimum transmission coefficients. In the oblique incidence case, the finesse will depend on the polarization state of the beam, since the value of "R", given by the Fresnel equations, is generally different for p and s polarizations.
A Fabry–Pérot interferometer differs from a Fabry–Pérot etalon in the fact that the distance ℓ between the plates can be tuned in order to change the wavelengths at which transmission peaks occur in the interferometer. Due to the angle dependence of the transmission, the peaks can also be shifted by rotating the etalon with respect to the beam.
Fabry–Pérot interferometers or etalons are used in optical modems, spectroscopy, lasers, and astronomy.
A related device is the Gires–Tournois etalon.
Detailed analysis
Two beams are shown in the diagram at the right, one of which (T0) is transmitted through the etalon, and the other of which (T1) is reflected twice before being transmitted. At each reflection, the amplitude is reduced by  and the phase is shifted by
and the phase is shifted by  , while at each transmission through an interface the amplitude is reduced by
, while at each transmission through an interface the amplitude is reduced by 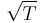 . Assuming no absorption, conservation of energy requires T + R = 1. In the derivation below, n is the index of refraction inside the etalon, and n0 is that outside the etalon. The incident amplitude at point a is taken to be one, and phasors are used to represent the amplitude of the radiation. The transmitted amplitude at point b will then be
. Assuming no absorption, conservation of energy requires T + R = 1. In the derivation below, n is the index of refraction inside the etalon, and n0 is that outside the etalon. The incident amplitude at point a is taken to be one, and phasors are used to represent the amplitude of the radiation. The transmitted amplitude at point b will then be
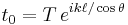 ,
,
where 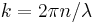 is the wavenumber inside the etalon and λ is the vacuum wavelength. At point c the transmitted amplitude will be
is the wavenumber inside the etalon and λ is the vacuum wavelength. At point c the transmitted amplitude will be
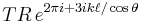 .
.
The total amplitude of both beams will be the sum of the amplitudes of the two beams measured along a line perpendicular to the direction of the beam. The amplitude at point b can therefore be added to an amplitude t1 equal in magnitude to the amplitude at point c, but retarded in phase by an amount k0 ℓ0 where 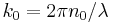 is the wavenumber outside of the etalon. Thus
is the wavenumber outside of the etalon. Thus
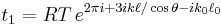 ,
,
where ℓ0 is
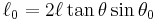 .
.
Neglecting the 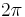 phase change due to the two reflections, the phase difference between the two beams is
phase change due to the two reflections, the phase difference between the two beams is
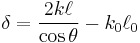 .
.
The relationship between θ and θ0 is given by Snell's law:
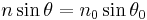 ,
,
so that the phase difference may be written:
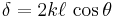 .
.
To within a constant multiplicative phase factor, the amplitude of the mth transmitted beam can be written as:
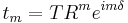 .
.
The total transmitted amplitude is the sum of all individual beams' amplitudes:
The series is a geometric series whose sum can be expressed analytically. The amplitude can be rewritten as
 .
.
The intensity of the beam will be just t times its complex conjugate. Since the incident beam was assumed to have an intensity of one, this will also give the transmission function:
Another expression for the transmission function
Defining 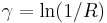 the above expression may be written as:
the above expression may be written as:
The second term is proportional to a wrapped Lorentzian distribution so that the transmission function may be written as a series of Lorentzian functions:
where
Applications
- The most important common applications are as dichroic filters, in which a series of etalonic layers are deposited on an optical surface by vapor deposition. These optical filters usually have more exact reflective and pass bands than absorptive filters. When properly designed, they run cooler than absorptive filters because they can reflect unwanted wavelengths. Dichroic filters are widely used in optical equipment such as light sources, cameras and astronomical equipment.
- Telecommunications networks employing wavelength division multiplexing have add-drop multiplexers with banks of miniature tuned fused silica or diamond etalons. These are small iridescent cubes about 2 mm on a side, mounted in small high-precision racks. The materials are chosen to maintain stable mirror-to-mirror distances, and to keep stable frequencies even when the temperature varies. Diamond is preferred because it has greater heat conduction and still has a low coefficient of expansion. In 2005, some telecommunications equipment companies began using solid etalons that are themselves optical fibers. This eliminates most mounting, alignment and cooling difficulties.
- An optical wavemeter is a combination of up to five Fabry–Pérot interferometers with a factor of ten difference in Δλ between any two of them. The beam is made divergent by a cylindrical lens and the distance between two bright lines is recorded by means of a CCD camera.
- Laser resonators are often described as Fabry–Pérot resonators, although for many types of laser the reflectivity of one mirror is close to 100%, making it more similar to a Gires–Tournois interferometer. Semiconductor diode lasers sometimes use a true Fabry–Pérot geometry, due to the difficulty of coating the end facets of the chip.
- Etalons are used to construct single-mode lasers. Without an etalon, a laser will generally produce light over a wavelength range corresponding to a number of cavity modes, which are similar to Fabry–Pérot modes. Inserting an etalon into the laser cavity, with well-chosen finesse and free-spectral range, can suppress all cavity modes except for one, thus changing the operation of the laser from multi-mode to single-mode.
- Fabry–Pérot etalons can be used to prolong the interaction length in laser absorption spectrometry techniques.
- A Fabry–Pérot etalon can be used to make a spectrometer capable of observing the Zeeman effect, where the spectral lines are far too close together to distinguish with a normal spectrometer.
- In astronomy an etalon is used to select a single atomic transition for imaging. The most common is the H-alpha line of the sun. The Ca-K line from the sun is also commonly imaged using etalons.
- In gravitational wave detection, a Fabry–Pérot cavity is used to store photons for almost a millisecond while they bounce up and down between the mirrors. This increases the time a gravitational wave can interact with the light, which results in a better sensitivity at low frequencies. This principle is used by detectors such as LIGO and Virgo, which consist of a Michelson interferometer with a Fabry–Pérot cavity with a length of several kilometers in both arms. Smaller cavities, usually called mode cleaners, are used for spatial filtering and frequency stabilization of the main laser.
See also
- Lummer–Gehrcke interferometer
- Atomic line filter
- ARROW waveguide
- Distributed Bragg reflector
- Fiber Bragg grating
- Thin-film interference
Notes and references
- ^ Perot frequently spelled his name with an accent—Pérot—in scientific publications, and so the name of the interferometer is commonly written with the accent. Métivier, Françoise (September–October 2006). "Jean-Baptiste Alfred Perot" (in French) (pdf). Photoniques (no. 25). http://www.sabix.org/documents/perot.pdf. Retrieved 2007-10-02. Page 2: "Pérot ou Perot?"
- ^ Oxford English Dictionary
- ^ Lipson, S.G.; Lipson, H.; Tannhauser, D.S. (1995). Optical Physics (3rd ed.). London: Cambridge U.P.. pp. 248. ISBN 0521069262.
- Hernandez, G. (1986). Fabry–Pérot Interferometers. Cambridge: Cambridge University Press. ISBN 0521322383.
External links
- Compact FP interferometer for gas analysis
- Advanced Design of Etalons- by Precision Photonics Corporation