FLOPS
| Name | FLOPS |
|---|---|
| yottaFLOPS | 1024 |
| zettaFLOPS | 1021 |
| exaFLOPS | 1018 |
| petaFLOPS | 1015 |
| teraFLOPS | 1012 |
| gigaFLOPS | 109 |
| megaFLOPS | 106 |
| kiloFLOPS | 103 |
In computing, FLOPS (or flops or flop/s, for floating-point operations per second) is a measure of a computer's performance, especially in fields of scientific calculations that make heavy use of floating-point calculations, similar to the older, simpler, instructions per second. Since the final S stands for "second", conservative speakers consider "FLOPS" as both the singular and plural of the term, although the singular "FLOP" is frequently encountered. Alternatively, the singular FLOP (or flop) is used as an abbreviation for "FLoating-point OPeration", and a flop count is a count of these operations (e.g., required by a given algorithm or computer program). In this context, "flops" is simply the plural rather than a rate.
Although it is in common use, FLOPS is not an SI unit. The expression 1 flops is actually interpreted as 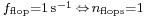 .
.
Contents |
Measuring performance
In order for FLOPS to be useful as a measure of floating-point performance, a standard benchmark must be available on all computers of interest. One example is the LINPACK benchmark.
There are many factors in computer performance other than raw floating-point computing speed, such as I/O performance, interprocessor communication, cache coherence, and the memory hierarchy. This means that supercomputers are in general only capable of a fraction of their "theoretical peak" FLOPS throughput (obtained by adding together the theoretical peak FLOPS performance of every element of the system). Even when operating on large highly parallel problems, their performance will be bursty, mostly due to the residual effects of Amdahl's law. Real benchmarks therefore measure both peak actual FLOPS performance as well as sustained FLOPS performance.
Supercomputer ratings, like TOP500, usually derive theoretical peak FLOPS as a product of number of cores, cycles per second each core runs at, and number of double-precision (64 bit) FLOPS each core can ideally perform, thanks to SIMD or otherwise. Despite different processor architectures can achieve different parallelism on single core, most mainstream ones, like recent Xeon and Itanium models, claim a factor of four. Some ratings adopted the factor as a given constant, and use it to compute peak values for all architectures, often leading to huge difference from sustained performance.
For ordinary (non-scientific) applications, integer operations (measured in MIPS) are far more common. Measuring floating-point operation speed, therefore, does not predict accurately how the processor will perform on just any problem. However, for many scientific jobs such as data analysis, a FLOPS rating is effective.
Historically, the earliest reliably documented serious use of the floating-point operation as a metric appears to be AEC justification to Congress for purchasing a Control Data CDC 6600 in the mid-1960s.
The terminology is currently so confusing that until April 24, 2006, U.S. export control was based upon measurement of "Composite Theoretical Performance" (CTP) in millions of "Theoretical Operations Per Second" or MTOPS. On that date, however, the U.S. Department of Commerce's Bureau of Industry and Security amended the Export Administration Regulations to base controls on Adjusted Peak Performance (APP) in Weighted TeraFLOPS (WT).
Records
NEC's SX-9 supercomputer was the world's first vector processor to exceed 100 gigaFLOPS per single core. IBM's supercomputer dubbed Roadrunner was the first to reach a sustained performance of 1 petaFLOPS, as measured by the Linpack benchmark. As of June 2011[update], the 500 fastest supercomputers in the world combine for 58.9 petaFLOPS of computing power.[1]
For comparison, a hand-held calculator performs relatively few FLOPS. Each calculation request, such as to add or subtract two numbers, requires only a single operation, so there is rarely any need for its response time to exceed what the operator can physically use. A computer response time below 0.1 second in a calculation context is usually perceived as instantaneous by a human operator,[2] so a simple calculator needs only about 10 FLOPS to be considered functional. In June 2006, a new computer was announced by Japanese research institute RIKEN, the MDGRAPE-3. The computer's performance tops out at one petaFLOPS, almost two times faster than the Blue Gene/L, but MDGRAPE-3 is not a general purpose computer, which is why it does not appear in the Top500.org list. It has special-purpose pipelines for simulating molecular dynamics.
By 2007, Intel Corporation unveiled the experimental multi-core POLARIS chip, which achieves 1 TFLOPS at 3.13 GHz. The 80-core chip can raise this result to 2 TFLOPS at 6.26 GHz, although the thermal dissipation at this frequency exceeds 190 watts.[3]
On June 26, 2007, IBM announced the second generation of its top supercomputer, dubbed Blue Gene/P and designed to continuously operate at speeds exceeding one petaFLOPS. When configured to do so, it can reach speeds in excess of three petaFLOPS.[4]
In June 2007, Top500.org reported the fastest computer in the world to be the IBM Blue Gene/L supercomputer, measuring a peak of 596 TFLOPS.[5] The Cray XT4 hit second place with 101.7 TFLOPS.
On October 25, 2007, NEC Corporation of Japan issued a press release[6] announcing its SX series model SX-9, claiming it to be the world's fastest vector supercomputer. The SX-9 features the first CPU capable of a peak vector performance of 102.4 gigaFLOPS per single core.
On February 4, 2008, the NSF and the University of Texas opened full scale research runs on an AMD, Sun supercomputer named Ranger,[7] the most powerful supercomputing system in the world for open science research, which operates at sustained speed of half a petaflop.
On May 25, 2008, an American military supercomputer built by IBM, named 'Roadrunner', reached the computing milestone of one petaflop by processing more than 1.026 quadrillion calculations per second. It headed the June 2008[8] and November 2008[9] TOP500 list of the most powerful supercomputers (excluding grid computers). The computer is located at Los Alamos National Laboratory in New Mexico, and the computer's name refers to the New Mexico state bird, the Greater Roadrunner.[10]
In June 2008, AMD released ATI Radeon HD4800 series, which are reported to be the first GPUs to achieve one teraFLOP scale. On August 12, 2008 AMD released the ATI Radeon HD 4870X2 graphics card with two Radeon R770 GPUs totaling 2.4 teraFLOPS.
In November 2008, an upgrade to the Cray XT Jaguar supercomputer at the Department of Energy’s (DOE’s) Oak Ridge National Laboratory (ORNL) raised the system's computing power to a peak 1.64 “petaflops,” or a quadrillion mathematical calculations per second, making Jaguar the world’s first petaflop system dedicated to open research. In early 2009 the supercomputer was named after a mythical creature, Kraken. Kraken was declared the world's fastest university-managed supercomputer and sixth fastest overall in the 2009 TOP500 list, which is the global standard for ranking supercomputers. In 2010 Kraken was upgraded and can operate faster and is more powerful.
In 2009, the Cray Jaguar performed at 1.75 petaFLOPS, beating the IBM Roadrunner for the number one spot on the TOP500 list.[11]
In October 2010, China unveiled the Tianhe-I, a supercomputer that operates at a peak computing rate of 2.5 petaflops.[12][13]
As of 2010[update], the fastest six-core PC processor reaches 109 GFLOPS (Intel Core i7 980 XE)[14] in double precision calculations. GPUs are considerably more powerful. For example, Nvidia Tesla C2050 GPU computing processors perform around 515 GFLOPS[15] in double precision calculations, and the AMD FireStream 9270 peaks at 240 GFLOPS.[16] In single precision performance, Nvidia Tesla C2050 computing processors perform around 1.03 TFLOPS and the AMD FireStream 9270 cards peak at 1.2 TFLOPS. Both Nvidia and AMD's consumer gaming GPUs may reach higher FLOPS. For example, AMD’s HemlockXT 5970[17] reaches 928 GFLOPS in double precision calculations with two GPUs on board and the Nvidia GTX 480 reaches 672 GFLOPS[18] with one GPU on board.
In November 2011, it was announced that Japan had achieved 10.51 petaflops with its K computer [19]. It is still under development and software performance tuning is currently underway. It has 88,128 SPARC64 VIIIfx processors in 864 racks, with theoretical performance of 11.28 petaflops. It is named after the Japanese word "kei", which stands for 10 quadrillion,[20] corresponding to the target speed of 10 petaflops.
On November 15, 2011, Intel demonstrated a single x86-based processor, code-named "Knights Corner," sustaining more than a TeraFlop on a wide range of DGEMM operations. Intel emphasized during the demonstration this was a sustained TeraFlop (not "raw TeraFlop" used by others to get higher but less meaningful numbers), and that it was the first general purpose processor to ever cross a TeraFlop.[21][22]
Distributed computing uses the Internet to link personal computers to achieve more FLOPS:
- Folding@Home is sustaining over 4.1 native petaFLOPS as of July 2011[23] or 6.6 x86 PFLOPS (x86 flops are an approximate measurement of the speed of a calculation on an x86-based processor, different from native flops[24]). It is the first computing project of any kind to cross the 1, 2, 3, 4, and 5 native petaFLOPS milestone. This level of performance is primarily enabled by the cumulative effort of a vast array of powerful GPU, PlayStation 3 and CPU units.[25]
- The entire BOINC network averages about 5.3 PFLOPS as of July 25, 2011[update].[26]
- As of July 2011[update], MilkyWay@Home computes at over 460 TFLOPS, with a large amount of this work coming from GPUs.[27]
- As of July 2011[update], SETI@Home, which began in 1999, computes data averages more than 500 TFLOPS.[28]
- As of July 2011[update], Einstein@Home is crunching more than 190 TFLOPS.[29]
- As of July 2011[update], GIMPS, which began in 1996, is sustaining 59 TFLOPS.[30]
Future developments
In 2008, James Bamford's The Shadow Factory reported that NSA told the Pentagon it would need an exaflop computer by 2018.[31]
In May 2008, a collaboration was announced between NASA, SGI, and Intel to build a 1 PFLOPS computer, Pleiades, in 2009, scaling up to 10 PFLOPS by 2012.[32] At the same time, IBM intended to build a 20 PFLOPS supercomputer, Sequoia, at Lawrence Livermore National Laboratory until 2011.
On December 2, 2010, the US Air Force unveiled a defense supercomputer made up of 1,760 Playstation 3 consoles that can run 500 trillion floating-point operations per second.[33] (500 TFLOPS)
On October 11, 2011, the Oak Ridge National Laboratory announced they were building a 20 petaflop supercomputer, named Titan, which will become operational in 2012, the hybrid Titan system will combine AMD Opteron processors with “Kepler” NVIDIA Tesla graphic processing unit (GPU) technologies.[34]
Given the current speed of progress, supercomputers are projected to reach 1 exaFLOPS (EFLOPS) in 2019.[35] Cray, Inc. announced in December 2009 a plan to build a 1 EFLOPS supercomputer before 2020.[36] Erik P. DeBenedictis of Sandia National Laboratories theorizes that a zettaFLOPS (ZFLOPS) computer is required to accomplish full weather modeling of two week time span.[37] Such systems might be built around 2030.[38]
In India, ISRO and Indian Institute of Science have planned to make a 132.8 exaflop supercomputer by 2017, 100 times faster than any supercomputer ever planned. It would cost US $2 billion, but the Indian Government is ready to provide funding and all key equipment is booked. ISRO Scientists say they have planned very carefully to put up such a target.[39]
Cost of computing
Hardware costs
The following is a list of examples of computers that demonstrates how drastically performance has increased and price has decreased. The "cost per GFLOPS" is the cost for a set of hardware that would theoretically operate at one billion floating-point operations per second. During the era when no single computing platform was able to achieve one GFLOPS, this table lists the total cost for multiple instances of a fast computing platform which speed sums to one GFLOPS. Otherwise, the least expensive computing platform able to achieve one GFLOPS is listed.
| Date | Approximate cost per GFLOPS | Technology | Comments |
|---|---|---|---|
| 1961 | US $1,100,000,000,000 ($1.1 trillion) | About 17 million IBM 1620 units costing $64,000 each | The 1620's multiplication operation takes 17.7 ms.[40] |
| 1984 | $15,000,000 | Cray X-MP | |
| 1997 | $30,000 | Two 16-processor Beowulf clusters with Pentium Pro microprocessors[41] | |
| April 2000 | $1,000 | Bunyip Beowulf cluster | Bunyip was the first sub-US$1/MFLOPS computing technology. It won the Gordon Bell Prize in 2000. |
| May 2000 | $640 | KLAT2 | KLAT2 was the first computing technology which scaled to large applications while staying under US$1/MFLOPS.[42] |
| August 2003 | $82 | KASY0 | KASY0 was the first sub-US$100/GFLOPS computing technology.[43] |
| August 2007 | $48 | Microwulf | As of August 2007, this 26.25 GFLOPS "personal" Beowulf cluster can be built for $1256.[44] |
| March 2011 | $1.80 | HPU4Science | This $30,000 cluster was built using only commercially available "gamer" grade hardware.[45] |
The trend toward placing ever more transistors inexpensively on an integrated circuit follows Moore's law. This trend explains the rising speed and falling cost of computer processing.
Operation costs
In energy cost, according to the Green500 list, as of June 2011[update] the most efficient TOP500 supercomputer runs at 2097.19 MFLOPS per watt. This translates to an energy requirement of 0.477 watts per GFLOPS, however this energy requirement will be much greater for less efficient supercomputers.
Hardware costs for low cost supercomputers may be less significant than energy costs when running continuously for several years.
Floating-point operation and integer operation
Floating-point operation per second or FLOPS, measures the computing ability of a computer. An example of a floating-point operation is the calculation of mathematical equations. FLOPS is a good indicator to measure performance on DSP, supercomputers, robotic motion control, and scientific simulations. MIPS is used to measure the integer performance of a computer. Examples of integer operation is data movement (A to B) or value testing (If A = B, then C). MIPS as a performance benchmark is adequate for the computer when it is used in database query, word processing, spreadsheets, or to run multiple virtual operating systems.[46][47] Frank H. McMahon, of the Lawrence Livermore National Laboratory (LLNL), invented the term FLOPS and MFLOPS (MegaFLOPS) so that he could compare the so-called Supercomputers of the day by the number of floating-point calculations they did per second. This was much better than using the prevalent MIPS (Millions of Instructions Per Second) to compare computers as this statistic usually had little bearing on the arithmetic capability of the machine.
Fixed-point (integers). These designations refer to the format used to store and manipulate numeric representations of data. Fixed-point are designed to represent and manipulate integers – positive and negative whole numbers – for example 16 bits, yielding up to 65,536 possible bit patterns (216).[48]
Floating-point (real numbers). The encoding scheme for floating-point numbers is more complicated than for fixed-point. The basic idea is the same as used in scientific notation, where a mantissa is multiplied by ten raised to some exponent. For instance, 5.4321 × 106, where 5.4321 is the mantissa and 6 is the exponent. Scientific notation is exceptional at representing very large and very small numbers. For example: 1.2 × 1050, the number of atoms in the earth, or 2.6 × 10−23, the distance a turtle crawls in one second compared to the diameter of our galaxy. Notice that numbers represented in scientific notation are normalized so that there is only a single nonzero digit left of the decimal point. This is achieved by adjusting the exponent as needed. Floating-point representation is similar to scientific notation, except everything is carried out in base two, rather than base ten. While several similar formats are in use, the most common is ANSI/IEEE Std. 754-1985. This standard defines the format for 32-bit numbers called single precision, as well as 64-bit numbers called double precision and longer numbers called extended precision (used for intermediate results). Floating-point representations can support a much wider range of values than fixed-point, with the ability to represent very small numbers and very large numbers.
With fixed-point notation, the gaps between adjacent numbers always equal a value of one, whereas in floating-point notation, gaps between adjacent numbers are not uniformly spaced—the gap between any two numbers is approximately ten million times smaller than the value of the numbers (ANSI/IEEE Std. 754 standard format), with large gaps between large numbers and small gaps between small numbers.[49]
Dynamic range and precision. The exponentiation inherent in floating-point computation assures a much larger dynamic range – the largest and smallest numbers that can be represented - which is especially important when processing data sets which are extremely large or where the range may be unpredictable. As such, floating-point processors are ideally suited for computationally intensive applications. It is also important to consider fixed and floating-point formats in the context of precision – the size of the gaps between numbers. Every time a processor generates a new number via a mathematical calculation, that number must be rounded to the nearest value that can be stored via the format in use. Rounding and/or truncating numbers during processing naturally yields quantization error or ‘noise’ - the deviation between actual values and quantized values. Since the gaps between adjacent numbers can be much larger with fixed-point processing when compared to floating-point processing, round-off error can be much more pronounced. As such, floating-point processing yields much greater precision than fixed-point processing, distinguishing floating-point processors as the ideal CPU when computing accuracy is a critical requirement.[50]
See also
References
- ^ "Number of Processors share for 06/2011". TOP500 Supercomputing Site. http://www.top500.org/stats/list/37/procclass. Retrieved June 23, 2011.
- ^ "Response Times: The Three Important Limits". Jakob Nielsen. http://www.useit.com/papers/responsetime.html. Retrieved June 11, 2008.
- ^ The Arrival of TeraFLOP Computing | bit-tech.net
- ^ "June 2008". TOP500. http://www.top500.org/lists/2008/06. Retrieved July 8, 2008.
- ^ "29th TOP500 List of World's Fastest Supercomputers Released". Top500.org. June 23, 2007. http://top500.org/news/2007/06/23/29th_top500_list_world_s_fastest_supercomputers_released. Retrieved July 8, 2008.
- ^ "NEC Launches World's Fastest Vector Supercomputer, SX-9". NEC. October 25, 2007. http://www.nec.co.jp/press/en/0710/2501.html. Retrieved July 8, 2008.
- ^ "University of Texas at Austin, Texas Advanced Computing Center". http://www.tacc.utexas.edu/resources/hpcsystems/. Retrieved September 13, 2010. "Any researcher at a U.S. institution can submit a proposal to request an allocation of cycles on the system."
- ^ Sharon Gaudin (June 9, 2008). "IBM's Roadrunner smashes 4-minute mile of supercomputing". Computerworld. http://www.computerworld.com/action/article.do?command=viewArticleBasic&taxonomyName=hardware&articleId=9095318&taxonomyId=12&intsrc=kc_top. Retrieved June 10, 2008.
- ^ Austin ISC08
- ^ Fildes, Jonathan (June 9, 2008). "Supercomputer sets petaflop pace". BBC News. http://news.bbc.co.uk/1/hi/technology/7443557.stm. Retrieved July 8, 2008.
- ^ Greenberg, Andy (November 16, 2009). "Cray Dethrones IBM In Supercomputing". Forbes. http://www.forbes.com/2009/11/15/supercomputer-ibm-jaguar-technology-cio-network-cray.html?feed=rss_popstories.
- ^ "China claims supercomputer crown". BBC News. October 28, 2010. http://www.bbc.co.uk/news/technology-11644252.
- ^ China Unveils 2.507-Petaflop Supercomputer, the World's Fastest | Popular Science
- ^ Intel's Core i7-980X Extreme Edition - Ready for Sick Scores?: Mathematics: Sandra Arithmetic, Crypto, Microsoft Excel - Techgage
- ^ NVIDIA Tesla Personal Supercomputer
- ^ AMD FireStream™ 9270 GPU Compute Accelerator
- ^ http://www.amd.com/us/products/desktop/graphics/ati-radeon-hd-5000/hd-5970/Pages/ati-radeon-hd-5970-specifications.aspx
- ^ GeForce GTX 480
- ^ http://www.fujitsu.com/global/news/pr/archives/month/2011/20111102-02.html
- ^ See Japanese numbers
- ^ "Intel's Knights Corner: 50+ Core 22nm Co-processor". http://www.tomshardware.com/news/intel-knights-corner-mic-co-processor,14002.html. Retrieved November 16, 2011.
- ^ "Intel unveils 1 TFLOP/s Knight's Corner". http://www.eetimes.com/electronics-news/4230654/Intel-unveils-1-TFLOP-s-Knight-s-Corner. Retrieved November 16, 2011.
- ^ "Client statistics by OS". Folding@Home. July 25, 2011. http://fah-web.stanford.edu/cgi-bin/main.py?qtype=osstats. Retrieved July 25, 2011.
- ^ "FLOP FAQ". Folding@Home. April 4, 2009. http://folding.stanford.edu/English/FAQ-flops. Retrieved March 22, 2011.
- ^ Staff (November 6, 2008). "Sony Computer Entertainment's Support for Folding@home Project on PlayStation3 Receives This Year's "Good Design Gold Award"". Sony Computer Entertainment Inc.. Sony Computer Entertainment Inc. (Sony Computer Entertainment Inc.). http://www.scei.co.jp/corporate/release/081106de.html. Retrieved December 11, 2008.
- ^ "Credit overview". BOINC. http://www.boincstats.com/stats/project_graph.php?pr=bo. Retrieved July 25, 2010.
- ^ "MilkyWay@Home Credit overview". BOINC. http://boincstats.com/stats/project_graph.php?pr=milkyway. Retrieved July 25, 2011.
- ^ "SETI@Home Credit overview". BOINC. http://www.boincstats.com/stats/project_graph.php?pr=sah. Retrieved July 25, 2011.
- ^ "Einstein@Home Credit overview". BOINC. http://de.boincstats.com/stats/project_graph.php?pr=einstein. Retrieved July 25, 2011.
- ^ "Internet PrimeNet Server Distributed Computing Technology for the Great Internet Mersenne Prime Search". GIMPS. http://www.mersenne.org/primenet. Retrieved July 25, 2011
- ^ p339, Shadow Factory, Bamford
- ^ "NASA collaborates with Intel and SGI on forthcoming petaflops super computers". Heise online. May 9, 2008. http://www.heise.de/english/newsticker/news/107683.
- ^ Air Force Unveils Fastest Defense Supercomputer, Made of 1,760 PlayStation 3s | Popular Science
- ^ http://www.informationweek.com/news/government/enterprise-architecture/231900554
- ^ Thibodeau, Patrick (June 10, 2008). "IBM breaks petaflop barrier". InfoWorld. http://www.infoworld.com/article/08/06/10/IBM_breaks_petaflop_barrier_1.html.
- ^ Cray studies exascale computing in Europe:
- ^ DeBenedictis, Erik P. (2005). "Reversible logic for supercomputing". Proceedings of the 2nd conference on Computing frontiers. New York, NY: ACM Press. pp. 391–402. ISBN 1595930191. http://portal.acm.org/citation.cfm?id=1062325.
- ^ "IDF: Intel says Moore's Law holds until 2029". Heise Online. April 4, 2008. http://www.h-online.com/newsticker/news/item/IDF-Intel-says-Moore-s-Law-holds-until-2029-734779.html.
- ^ "India to make World's Fastest Supercomputer". http://www.defencenews.in/defence-news-internal.asp?get=new&id=500.
- ^ IBM 1961 BRL Report
- ^ Loki and Hyglac
- ^ The Aggregate
- ^ The Aggregate - KASY0
- ^ Microwulf: A Personal, Portable Beowulf Cluster
- ^ Adam Stevenson, Yann Le Du, and Mariem El Afrit. "High-performance computing on gamer PCs." Ars Technica. March 31, 2011.
- ^ Fixed versus floating point. Retrieved on December 25, 2009.
- ^ Data manipulation and math calculation. Retrieved on December 25, 2009.
- ^ Integer Retrieved on December 25, 2009.
- ^ Floating Point Retrieved on December 25, 2009.
- ^ Summary: Fixed-point (integer) vs floating-point Retrieved on December 25, 2009.
External links
- Current Einstein@Home benchmark
- BOINC projects global benchmark
- Current GIMPS throughput
- Top500.org
- LinuxHPC.org Linux High Performance Computing and Clustering Portal
- WinHPC.org Windows High Performance Computing and Clustering Portal
- Oscar Linux-cluster ranking list by CPUs/types and respective FLOPS
- Information on how to calculate "Composite Theoretical Performance" (CTP)
- Information on the Oak Ridge National Laboratory Cray XT system.
- Infiscale Cluster Portal - Free GPL HPC
- Source code, pre-compiled versions and results for PCs - Linpack, Livermore Loops, Whetstone MFLOPS
- PC CPU Performance Comparisons %MFLOPS/MHz - CPU, Caches and RAM
- Xeon export compliance metrics, including GFLOPS
- IBM Brings NVIDIA Tesla GPUs Onboard (May 2010)