F1 score
In statistics, the F1 score (also F-score or F-measure) is a measure of a test's accuracy. It considers both the precision p and the recall r of the test to compute the score: p is the number of correct results divided by the number of all returned results and r is the number of correct results divided by the number of results that should have been returned. The F1 score can be interpreted as a weighted average of the precision and recall, where an F1 score reaches its best value at 1 and worst score at 0.
The traditional F-measure or balanced F-score (F1 score) is the harmonic mean of precision and recall:
 .
.
The general formula for positive real β is:
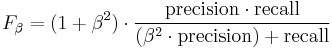 .
.
The formula in terms of Type I and type II errors:
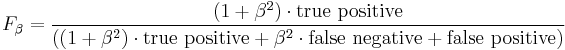 .
.
Two other commonly used F measures are the 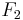 measure, which weights recall higher than precision, and the
measure, which weights recall higher than precision, and the 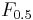 measure, which puts more emphasis on precision than recall.
measure, which puts more emphasis on precision than recall.
The F-measure was derived so that 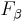 "measures the effectiveness of retrieval with respect to a user who attaches β times as much importance to recall as precision" [1]. It is based on van Rijsbergen's effectiveness measure
"measures the effectiveness of retrieval with respect to a user who attaches β times as much importance to recall as precision" [1]. It is based on van Rijsbergen's effectiveness measure
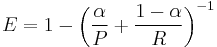 .
.
Their relationship is 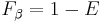 where
where 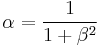 .
.
Applications
The F-score is often used in the field of information retrieval for measuring search, document classification, and query classification performance[2]. Earlier works focused primarily on the F1 score, but with the proliferation of large scale search engines, performance goals changed to place more emphasis on either precision or recall[3] and so 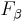 is seen in wide application.
is seen in wide application.
The F-score is also used in machine learning.[4] Note, however, that the F-measures do not take the true negative rate into account, and that measures such as the Matthews correlation coefficient may be preferable to assess the performance of a binary classifier.
See also
- BLEU
- NIST (metric)
- METEOR
- ROUGE (metric)
- Word Error Rate (WER)
- Noun phrase chunking
- Receiver operating characteristic
- Matthews correlation coefficient
References
- ^ van Rijsbergen, C. J. (1979). Information Retrieval (2nd ed.). Butterworth.
- ^ Steven M. Beitzel. (2006). On Understanding and Classifying Web Queries. Phd Thesis. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.127.634&rep=rep1&type=pdf.
- ^ X. Li, Y.-Y. Wang, and A. Acero (July 2008). "Learning query intent from regularized click graphs". Proceedings of the 31st SIGIR Conference.
- ^ See, e.g., the evaluation of the CoNLL 2002 shared task.