Exponentially closed field
In mathematics, an exponentially closed field is an ordered field 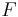 which has an order preserving isomorphism
which has an order preserving isomorphism 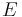 of the additive group of
of the additive group of 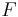 onto the multiplicative group of positive elements of
onto the multiplicative group of positive elements of 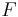 such that
such that 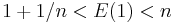 for some natural number
for some natural number 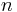 .
.
Isomorphism 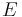 is called an exponential function in
is called an exponential function in 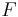 .
.
Contents |
Examples
- The canonical example for an exponentially closed field is the ordered field of real numbers; here
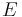 can be any function
can be any function 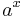 where
where 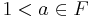 .
.
Properties
- Every exponentially closed field
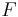 is root-closed, i.e., every positive element of
is root-closed, i.e., every positive element of 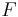 has an
has an 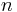 -th root for all positive integer
-th root for all positive integer 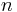 (or in other words the multiplicative group of positive elements of
(or in other words the multiplicative group of positive elements of 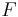 is divisible). This is so because
is divisible). This is so because 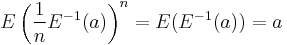 for all
for all 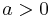 .
. - Consequently, every exponentially closed field is an Euclidean field.
- Consequently, every exponentially closed field is an ordered Pythagorean field.
- Not every real-closed field is an exponentially closed field, e.g., the field of real algebraic numbers is not exponentially closed. This is so because
 has to be
has to be 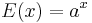 for some
for some 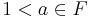 in every exponentially closed subfield
in every exponentially closed subfield 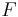 of the real numbers; and
of the real numbers; and 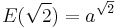 is not algebraic if
is not algebraic if 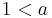 is algebraic by Gelfond–Schneider theorem.
is algebraic by Gelfond–Schneider theorem. - Consequently, the class of exponentially closed fields is not an elementary class since the field of real numbers and the field of real algebraic numbers are elementarily equivalent structures.
- The class of exponentially closed fields is a pseudoelementary class. This is so since a field
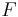 is exponentially closed iff there is a surjective function
is exponentially closed iff there is a surjective function 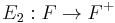 such that
such that 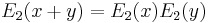 and
and 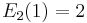 ; and these properties of
; and these properties of 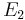 are axiomatizable.
are axiomatizable.
See also
- Ordered exponential fields
- Exponential fields
References
Norman L. Alling, "On Exponentially Closed Fields," Proceedings of the American Mathematical Society, Vol. 13, No. 5, 1962, pp.706--711. http://www.jstor.org/pss/2034159