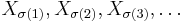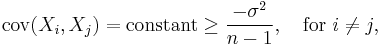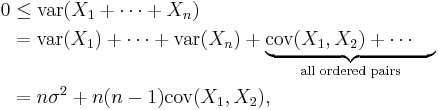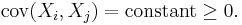Exchangeable random variables

In statistics, an exchangeable sequence of random variables (also sometimes interchangeable) is a sequence such that future samples behave like earlier samples, meaning formally that any order (of a finite number of samples) is equally likely. This formalizes the notion of "the future being predictable on the basis of past experience."

A sequence of independent and identically-distributed random variables (i.i.d.) is exchangeable, but so is sampling without replacement, which is not independent.

The notion is central to Bruno de Finetti's development of predictive inference and to Bayesian statistics — where frequentist statistics uses i.i.d. variables (samples from a population), Bayesian statistics more frequently uses exchangeable sequences. They are a key way in which Bayesian inference is "data-centric" (based on past and future observations), rather than "model-centric", as exchangeable sequences that are not i.i.d. cannot be modeled as "sampling from a fixed population".

1 Definition
2 Examples
3 Properties
4 Applications
5 See also
6 References

Definition

Formally, an exchangeable sequence of random variables is a finite or infinite sequence X₁, X₂, X₃, ... of random variables such that for any finite permutation σ of the indices 1, 2, 3, ..., i.e. any permutation σ that leaves all but finitely many indices fixed, the joint probability distribution of the permuted sequence

$X_{\sigma(1)}, X_{\sigma(2)}, X_{\sigma(3)}, \dots$

is the same as the joint probability distribution of the original sequence.

A sequence E₁, E₂, E₃, ... of events is said to be exchangeable precisely if the sequence of its indicator functions is exchangeable.

Independent and identically distributed random variables are exchangeable.

The distribution function F_{X₁,...,X_n}(x₁, ... ,x_n) of a finite sequence of exchangeable random variables is symmetric in its arguments x₁, ... ,x_n.

Examples

Any weighted average of iid sequences of random variables is exchangeable. See in particular de Finetti's theorem.

Suppose an urn contains n red and m blue marbles. Suppose marbles are drawn without replacement until the urn is empty. Let X_i be the indicator random variable of the event that the ith marble drawn is red. Then {X_i}_i=1,...n is an exchangeable sequence. This sequence cannot be extended to any longer exchangeable sequence.

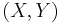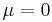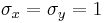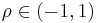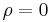Let $(X, Y)$ have a bivariate normal distribution with parameters $\mu = 0$ , $\sigma_x = \sigma_y = 1$ and an arbitrary correlation coefficient $\rho\in (-1, 1)$ . The random variables $X$ and $Y$ are then exchangeable, but independent only if $\rho=0$ . The density function is $p(x, y) = p(y, x) \propto \exp\left[-\frac{1}{2(1-\rho^2)}(x^2%2By^2-2\rho xy)\right].$

Properties

de Finetti's theorem characterizes exchangeable sequences as mixtures of i.i.d. sequences — while an exchangeable sequence need not itself be i.i.d., it can be expressed as a mixture of underlying i.i.d. sequences.

An infinite exchangeable sequence is strictly stationary, thus a law of large numbers in the form of Birkhoff-Khinchin theorem applies.

Covariance: for a finite exchangeable sequence { X_i }_{i = 1, 2, 3, ...} of length n:

$\operatorname{cov} (X_i,X_j) = \text{constant} \ge \frac{-\sigma^2}{n-1},\quad\text{for }i \ne j,$

where σ² = var(X₁).

"Constant" in this case means not depending on the values of the indices i and j as long as i ≠ j.

This may be seen as follows:

$\begin{align} 0 & \le \operatorname{var}(X_1 %2B \cdots %2B X_n) \\ & = \operatorname{var}(X_1) %2B \cdots %2B \operatorname{var}(X_n) %2B \underbrace{\operatorname{cov}(X_1,X_2) %2B \cdots\quad{}}_\text{all ordered pairs} \\ & = n\sigma^2 %2B n(n-1)\operatorname{cov}(X_1,X_2), \end{align}$

and then solve the inequality for the covariance. Equality is achieved in a simple urn model: An urn contains 1 red marble and n − 1 green marbles, and these are sampled without replacement until the urn is empty. Let X_i = 1 if the red marble is drawn on the ith trial and 0 otherwise.

A finite sequence that achieves the lower covariance bound cannot be extended to a longer exchangeable sequence.

For an infinite exchangeable sequence,

$\operatorname{cov} (X_i,X_j) = \text{constant} \ge 0.\,$

Applications

The von Neumann extractor is a randomness extractor that depends on exchangeability: it gives a method to take an exchangeable sequence of 0s and 1s (Bernoulli trials), with some probability p of 0 and 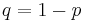$q=1-p$ of 1, and produce a (shorter) exchangeable sequence of 0s and 1s with probability 1/2.

Partition the sequence into non-overlapping pairs: if the two elements of the pair are equal (00 or 11), discard it; if the two elements of the pair are unequal (01 or 10), keep the first. This yields a sequence of Bernoulli trials with 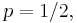$p=1/2,$ as, by exchangeability, the odds of a given pair being 01 or 10 are equal.

References

Aldous, David J., Exchangeability and related topics, in: École d'Été de Probabilités de Saint-Flour XIII — 1983, Lecture Notes in Math. 1117, pp. 1–198, Springer, Berlin, 1985. ISBN 978-3-540-15203-3 doi:10.1007/BFb0099421
Kingman, J. F. C., Uses of exchangeability, Ann. Probability 6 (1978) 83–197 MR 494344 JSTOR 2243211
Chow, Yuan Shih and Teicher, Henry, Probability theory. Independence, interchangeability, martingales, Springer Texts in Statistics, 3rd ed., Springer, New York, 1997. xxii+488 pp. ISBN 0-387-98228-0
Spizzichino, Fabio Subjective probability models for lifetimes. Monographs on Statistics and Applied Probability, 91. Chapman & Hall/CRC, Boca Raton, FL, 2001. xx+248 pp. ISBN 1-58488-060-0