Exact differential
A mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q.
The form A(x, y, z) dx + B(x, y, z) dy + C(x, y, z) dz is called a differential form. A differential form is exact on a domain D in space if A dx + B dy + C dz = df for some scalar function f throughout D. This is equivalent to saying that the field is conservative.
Contents |
Overview
For one dimension, a differential
is always exact.
For two dimensions, in order that a differential
be an exact differential in a simply-connected region R of the xy-plane, it is necessary and sufficient that between A and B there exists the relation:
For three dimensions, a differential
is an exact differential in a simply-connected region R of the xyz-coordinate system if between the functions A, B and C there exist the relations:
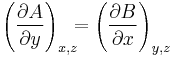 ;
;  ;
; 
-
- Note: The subscripts outside the parenthesis indicate which variables are being held constant during differentiation. Due to the definition of the partial derivative, these subscripts are not required, but they are included as a reminder.
These conditions are equivalent to the following one: If G is the graph of this vector valued function then for all tangent vectors X,Y of the surface G then s(X, Y) = 0 with s the symplectic form.
These conditions, which are easy to generalize, arise from the independence of the order of differentiations in the calculation of the second derivatives. So, in order for a differential dQ, that is a function of four variables to be an exact differential, there are six conditions to satisfy.
In summary, when a differential dQ is exact:
- the function Q exists;
 independent of the path followed.
independent of the path followed.
In thermodynamics, when dQ is exact, the function Q is a state function of the system. The thermodynamic functions U, S, H, A and G are state functions. Generally, neither work nor heat is a state function. An exact differential is sometimes also called a 'total differential', or a 'full differential', or, in the study of differential geometry, it is termed an exact form.
Partial differential relations
For three variables,  ,
,  and
and  bound by some differentiable function
bound by some differentiable function  , the following total differentials exist[1]:667&669
, the following total differentials exist[1]:667&669
Substituting the first equation into the second and rearranging, we obtain[1]:669
Since  and
and  are independent variables,
are independent variables, 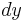 and
and 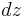 may be chosen without restriction. For this last equation to hold in general, the bracketed terms must be equal to zero.[1]:669
may be chosen without restriction. For this last equation to hold in general, the bracketed terms must be equal to zero.[1]:669
Reciprocity relation
Setting the first term in brackets equal to zero yields[1]:670
A slight rearrangement gives a reciprocity relation,[1]:670
There are two more permutations of the foregoing derivation that give a total of three reciprocity relations between  ,
,  and
and  . Reciprocity relations show that the inverse of a partial derivative is equal to its reciprocal.
. Reciprocity relations show that the inverse of a partial derivative is equal to its reciprocal.
Cyclic relation
The cyclic relation is also known as the cyclic rule or the Triple product rule. Setting the second term in brackets equal to zero yields[1]:670
Using a reciprocity relation for  on this equation and reordering gives a cyclic relation (the triple product rule),[1]:670
on this equation and reordering gives a cyclic relation (the triple product rule),[1]:670
If, instead, a reciprocity relation for  is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
Some useful equations derived from exact differentials in two dimensions
(See also Bridgman's thermodynamic equations for the use of exact differentials in the theory of thermodynamic equations)
Suppose we have five state functions  , and
, and  . Suppose that the state space is two dimensional and any of the five quantities are exact differentials. Then by the chain rule
. Suppose that the state space is two dimensional and any of the five quantities are exact differentials. Then by the chain rule

but also by the chain rule:

and
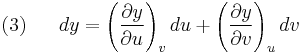
so that:
![(4)~~~~~
dz =
\left[
\left(\frac{\partial z}{\partial x}\right)_y
\left(\frac{\partial x}{\partial u}\right)_v
%2B
\left(\frac{\partial z}{\partial y}\right)_x
\left(\frac{\partial y}{\partial u}\right)_v
\right]du](/2012-wikipedia_en_all_nopic_01_2012/I/eb4403091698adde7d61fa6caed95c8c.png)
which implies that:

Letting  gives:
gives:
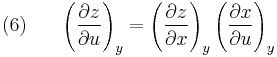
Letting 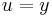 gives:
gives:

Letting 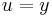 ,
,  gives:
gives:

using ( gives the triple product rule:
gives the triple product rule:

See also
- Closed and exact differential forms for a higher-level treatment
- Differential (mathematics)
- Inexact differential
- Integrating factor for solving non-exact differential equations by making them exact
- Exact differential equation
References
- ^ a b c d e f g Çengel, Yunus A.; Boles, Michael A. (1998) [1989]. "Thermodynamics Property Relations". Thermodynamics - An Engineering Approach. McGraw-Hill Series in Mechanical Engineering (3rd ed.). Boston, MA.: McGraw-Hill. ISBN 0-07-011927-9.
- Perrot, P. (1998). A to Z of Thermodynamics. New York: Oxford University Press.
- Zill, D. (1993). A First Course in Differential Equations, 5th Ed. Boston: PWS-Kent Publishing Company.
External links
- Inexact Differential – from Wolfram MathWorld
- Exact and Inexact Differentials – University of Arizona
- Exact and Inexact Differentials – University of Texas
- Exact Differential – from Wolfram MathWorld






![d z = {\left ( \frac{\partial z}{\partial x} \right )}_y \left [ {\left ( \frac{\partial x}{\partial y} \right )}_z d y %2B {\left ( \frac{\partial x}{\partial z} \right )}_y dz \right ] %2B {\left ( \frac{\partial z}{\partial y} \right )}_x dy,](/2012-wikipedia_en_all_nopic_01_2012/I/7cf71cf5a01f35dd85ac4ea11cfc513b.png)
![d z = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z %2B {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y %2B {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y dz,](/2012-wikipedia_en_all_nopic_01_2012/I/f451c5d4f9b73c6a9ea23aebe0eefbd3.png)
![\left [ 1 - {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y \right ] dz = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z %2B {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y.](/2012-wikipedia_en_all_nopic_01_2012/I/94185246967c1bd97614b63499f22d6e.png)


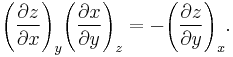


![%2B
\left[
\left(\frac{\partial z}{\partial x}\right)_y
\left(\frac{\partial x}{\partial v}\right)_u
%2B
\left(\frac{\partial z}{\partial y}\right)_x
\left(\frac{\partial y}{\partial v}\right)_u
\right]dv](/2012-wikipedia_en_all_nopic_01_2012/I/0502fc18d6b162fda0d70f94a537a388.png)