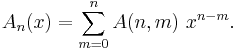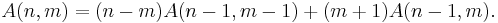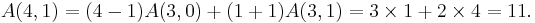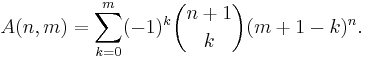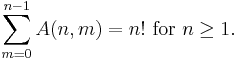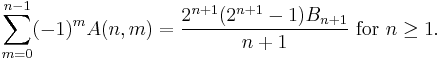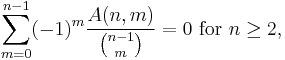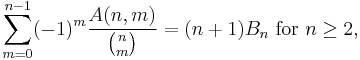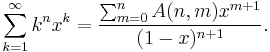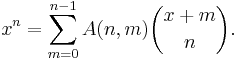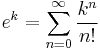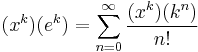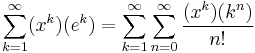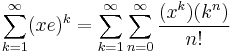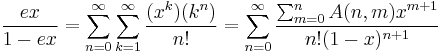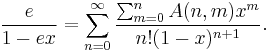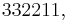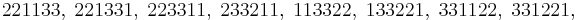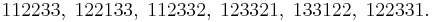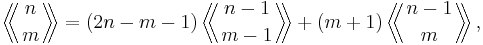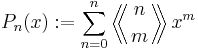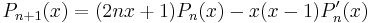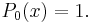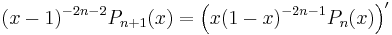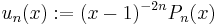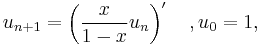Eulerian number
In combinatorics the Eulerian number A(n, m), is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element (permutations with m "ascents"). They are the coefficients of the Eulerian polynomials:
This polynomial appears as the numerator in an expression for the generating function of the sequence 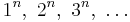 .
.
Other notations for A(n, m) are E(n, m) and 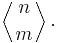
Contents |
History
In 1755 Leonhard Euler investigated in his book Institutiones calculi differentialis polynomials α1(x) = 1, α2(x) = x + 1, α3(x) = x2 + 4x + 1, etc. (see the facsimile). These polynomials are a shifted form of what are now called the Eulerian polynomials An(x).
Basic properties
For a given value of n > 0, the index m in A(n, m) can take values from 0 to n − 1. For fixed n there is a single permutation which has 0 ascents; this is the falling permutation (n, n − 1, n − 2, ..., 1). There is also a single permutation which has n − 1 ascents; this is the rising permutation (1, 2, 3, ..., n). Therefore A(n, 0) and A(n, n − 1) are 1 for all values of n.
Reversing a permutation with m ascents creates another permutation in which there are n − m − 1 ascents. Therefore A(n, m) = A(n, n − m − 1).
Values of A(n, m) can be calculated "by hand" for small values of n and m. For example
-
n m Permutations A(n, m) 1 0 (1) A(1,0) = 1 2 0 (2, 1) A(2,0) = 1 1 (1, 2) A(2,1) = 1 3 0 (3, 2, 1) A(3,0) = 1 1 (1, 3, 2) (2, 1, 3) (2, 3, 1) (3, 1, 2) A(3,1) = 4 2 (1, 2, 3) A(3,2) = 1
For larger values of n, A(n, m) can be calculated using the recursion formula
For example
Values of A(n, m) (sequence A008292 in OEIS) for 0 ≤ n ≤ 9 are:
-
n \ m 0 1 2 3 4 5 6 7 8 1 1 2 1 1 3 1 4 1 4 1 11 11 1 5 1 26 66 26 1 6 1 57 302 302 57 1 7 1 120 1191 2416 1191 120 1 8 1 247 4293 15619 15619 4293 247 1 9 1 502 14608 88234 156190 88234 14608 502 1
The above triangular array is called the Euler triangle or Euler's triangle, and it shares some common characteristics with Pascal's triangle. The sum of row n is the factorial n!.
Closed-form expression
A closed-form expression for A(n, m) is
Summation properties
It is clear from the combinatoric definition that the sum of the Eulerian numbers for a fixed value of n is the total number of permutations of the numbers 1 to n, so
The alternating sum of the Eulerian numbers for a fixed value of n is related to the Bernoulli number Bn+1
Other summation properties of the Eulerian numbers are:
where Bn is the nth Bernoulli number.
Identities
The Eulerian numbers are involved in the generating function for the sequence of nth powers
Worpitzky's identity expresses xn as the linear combination of Eulerian numbers with binomial coefficients:
Another interesting identity is given by the following manipulation:
So for 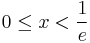 we have that the terms on the right side are positive, so we may switch the sum. The terms on the left make a geometric series, and we know that converges. After all of that, we use the above identity to finish the manipulation:
we have that the terms on the right side are positive, so we may switch the sum. The terms on the left make a geometric series, and we know that converges. After all of that, we use the above identity to finish the manipulation:
Finally, for 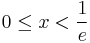 we get
we get
Notice that the sum on the right-hand side is the sum of the Eulerian polynomials shown at the top of this page.
Eulerian numbers of the second kind
The permutations of the multiset 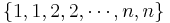 which have the property that for each k, all the numbers appearing between the two occurrences of k in the permutation are greater than k are counted by the double factorial number (2n-1)!!. The Eulerian number of the second kind, denoted
which have the property that for each k, all the numbers appearing between the two occurrences of k in the permutation are greater than k are counted by the double factorial number (2n-1)!!. The Eulerian number of the second kind, denoted 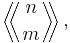 counts the number of all such permutations that have exactly m ascents. For instance, for n=3 there are 15 such permutations, 1 with no ascents, 8 with a single ascent, and 6 with two ascents:
counts the number of all such permutations that have exactly m ascents. For instance, for n=3 there are 15 such permutations, 1 with no ascents, 8 with a single ascent, and 6 with two ascents:
The Eulerian numbers of the second kind 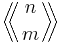 satisfy the recurrence relation, that follows directly from the above definition:
satisfy the recurrence relation, that follows directly from the above definition:
with initial condition for n=0, expressed in Iverson bracket notation:
![\left \langle \!\!\left \langle {0\atop m} \right \rangle \!\! \right \rangle = [m=0]](/2012-wikipedia_en_all_nopic_01_2012/I/3dd80f136ff2011ccc74b79496c6bbdd.png) .
.
Correspondingly, the Eulerian polynomial of second kind, here denoted 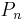 (no standard notation exists for them) are
(no standard notation exists for them) are
and the above recurrence relations are translated into a recurrence relation for the sequence Pn(x):
with initial condition
The latter recurrence may be written in a somehow more compact form by means of an integrating factor:
so that the rational function
satisfies a simple autonomous recurrence:
whence one obtains the Eulerian polynomials as Pn(x)=(1-x)2nun(x), and the Eulerian numbers of the second kind as their coefficients.
Here are some values of the second order Eulerian numbers (sequence A008517 in OEIS):
-
n \ m 0 1 2 3 4 5 6 7 8 1 1 2 1 2 3 1 8 6 4 1 22 58 24 5 1 52 328 444 120 6 1 114 1452 4400 3708 720 7 1 240 5610 32120 58140 33984 5040 8 1 494 19950 195800 644020 785304 341136 40320 9 1 1004 67260 1062500 5765500 12440064 11026296 3733920 362880
The sum of the n-th row, which is also the value Pn(1), is then (2n-1)!!.
References
- Leonardus Eulerus (Leonhard Euler) (1755). Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum (Foundations of Differential Calculus, with Applications to Finite Analysis and Series). Academia imperialis scientiarum Petropolitana; Berolini: Michaelis.
- Graham, Knuth, Patashnik (1994). Concrete Mathematics: A Foundation for Computer Science, Second Edition. Addison-Wesley, pp. 267–272.
External links
- Eulerian Polynomials at OEIS Wiki.
- "Eulerian Numbers" at MathPages.com.
- Weisstein, Eric W., "Eulerian Number" from MathWorld.
- Weisstein, Eric W., "Euler's Number Triangle" from MathWorld.
- Weisstein, Eric W., "Worpitzky's Identity" from MathWorld.
- Weisstein, Eric W., "Second-Order Eulerian Triangle" from MathWorld.
- Euler-matrix (generalized rowindexes, divergent summation)