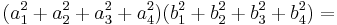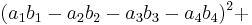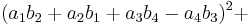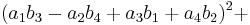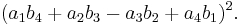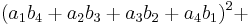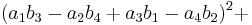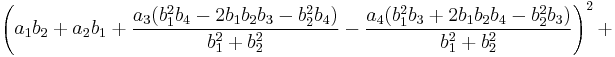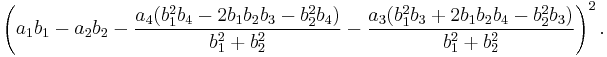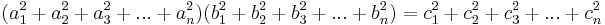Euler's four-square identity
In mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:
Euler wrote about this identity in a letter dated May 4, 1748 to Goldbach[1][2] (but note that he used a different sign convention from the above). It can be proven with elementary algebra and holds in every commutative ring. If the 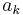 and
and 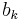 are real numbers, a more elegant proof is available: the identity expresses the fact that the absolute value of the product of two quaternions is equal to the product of their absolute values, in the same way that the Brahmagupta-Fibonacci two-square identity does for complex numbers.
are real numbers, a more elegant proof is available: the identity expresses the fact that the absolute value of the product of two quaternions is equal to the product of their absolute values, in the same way that the Brahmagupta-Fibonacci two-square identity does for complex numbers.
The identity was used by Lagrange to prove his four square theorem. More specifically, it implies that it is sufficient to prove the theorem for prime numbers, after which the more general theorem follows. The sign convention used above corresponds to the signs obtained by multiplying two quaternions. Other sign conventions can be obtained by changing any 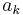 to
to 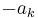 ,
, 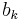 to
to 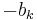 , or by changing the signs inside any of the squared terms on the right hand side.
, or by changing the signs inside any of the squared terms on the right hand side.
However, a different kind of four-square identity can be given as,
More generally, while Hurwitz's theorem states that an identity of form,
where the 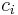 are bilinear functions of the
are bilinear functions of the 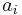 and
and 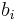 is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the
is possible only for n = {1, 2, 4, 8}, the more general Pfister's theorem allows that if the 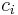 are just rational functions of one set of variables (in this case, the
are just rational functions of one set of variables (in this case, the 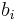 ), hence has a denominator, then it is possible for all
), hence has a denominator, then it is possible for all 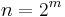 .[3]
.[3]
- Euler's Four Square Identity can be further Generalized by letting
A,B, and C be the Coefficients of four Binary Quartic Forms, whose Variables are 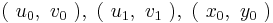 , and
, and 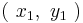
Also let 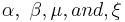 be any quantities desired. Then
be any quantities desired. Then
The derivation of this is done in pure algebra. The algebra needed to derive this Identity can be found in a PDF file called the Generalization of Euler's Four Squares (about 60 pages ). It can be found at http://www.samz.us
Notice that we have Euler's Identity by letting 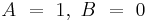 , and
, and 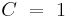 , and
, and 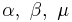 , and,
, and, 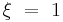
See also
References
- ^ Leonhard Euler: Life, Work and Legacy, R.E. Bradley and C.E. Sandifer (eds), Elsevier, 2007, p. 193
- ^ Mathematical Evolutions, A. Shenitzer and J. Stillwell (eds), Math. Assoc. America, 2002, p. 174
- ^ Pfister's Theorem on Sums of Squares, Keith Conrad, http://www.math.uconn.edu/~kconrad/blurbs/linmultialg/pfister.pdf
External links
- A Collection of Algebraic Identities
- [1] Lettre CXV from Euler to Goldbach