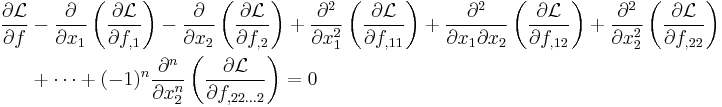Euler–Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation,[1] or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary. It was developed by Swiss mathematician Leonhard Euler and Italian mathematician Joseph Louis Lagrange in the 1750s.
Because a differentiable functional is stationary at its local maxima and minima, the Euler–Lagrange equation is useful for solving optimization problems in which, given some functional, one seeks the function minimizing (or maximizing) it. This is analogous to Fermat's theorem in calculus, stating that where a differentiable function attains its local extrema, its derivative is zero.
In Lagrangian mechanics, because of Hamilton's principle of stationary action, the evolution of a physical system is described by the solutions to the Euler–Lagrange equation for the action of the system. In classical mechanics, it is equivalent to Newton's laws of motion, but it has the advantage that it takes the same form in any system of generalized coordinates, and it is better suited to generalizations (see, for example, the "Field theory" section below).
Contents |
History
The Euler–Lagrange equation was developed in the 1750s by Euler and Lagrange in connection with their studies of the tautochrone problem. This is the problem of determining a curve on which a weighted particle will fall to a fixed point in a fixed amount of time, independent of the starting point.
Lagrange solved this problem in 1755 and sent the solution to Euler. The two further developed Lagrange's method and applied it to mechanics, which led to the formulation of Lagrangian mechanics. Their correspondence ultimately led to the calculus of variations, a term coined by Euler himself in 1766.[2]
Statement
The Euler–Lagrange equation is an equation satisfied by a function, q, of a real argument, t, which is a stationary point of the functional
where:
- q is the function to be found:
- such that q is differentiable, q(a) = xa, and q(b) = xb;
- q′ is the derivative of q:
- TX being the tangent bundle of X (the space of possible values of derivatives of functions with values in X);
- L is a real-valued function with continuous first partial derivatives:
The Euler–Lagrange equation, then, is given by
where Lx and Lv denote the partial derivatives of L with respect to the second and third arguments, respectively.
If the dimension of the space X is greater than 1, this is a system of differential equations, one for each component:
-
Derivation of one-dimensional Euler–Lagrange equation The derivation of the one-dimensional Euler–Lagrange equation is one of the classic proofs in mathematics. It relies on the fundamental lemma of calculus of variations.
We wish to find a function
 which satisfies the boundary conditions
which satisfies the boundary conditions 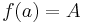 ,
, 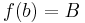 , and which extremizes the functional
, and which extremizes the functionalWe assume that
 has continuous first partial derivatives. A weaker assumption can be used, but the proof becomes more difficult.
has continuous first partial derivatives. A weaker assumption can be used, but the proof becomes more difficult.If
 extremizes the functional subject to the boundary conditions, then any slight perturbation of
extremizes the functional subject to the boundary conditions, then any slight perturbation of  that preserves the boundary values must either increase
that preserves the boundary values must either increase  (if
(if  is a minimizer) or decrease
is a minimizer) or decrease  (if
(if  is a maximizer).
is a maximizer).Let
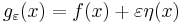 be the result of such a perturbation
be the result of such a perturbation 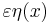 of
of  , where
, where 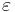 is small and
is small and 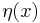 is a differentiable function satisfying
is a differentiable function satisfying 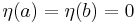 . Then define
. Then definewhere
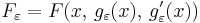 .
.We now wish to calculate the total derivative of
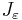 with respect to ε.
with respect to ε.It follows from the total derivative that
So
When ε = 0 we have gε = f , Fε = F(x, f(x), f'(x)) and Jε has an extremum value, so that
The next step is to use integration by parts on the second term of the integrand, yielding
Using the boundary conditions
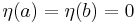 ,
,Applying the fundamental lemma of calculus of variations now yields the Euler–Lagrange equation
-
Alternate derivation of one-dimensional Euler–Lagrange equation Given a functional
on
![C^1([a, b])](/2012-wikipedia_en_all_nopic_01_2012/I/8a33eba68d7379b365730528445287cb.png) with the boundary conditions
with the boundary conditions 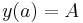 and
and 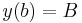 , we proceed by approximating the extremal curve by a polygonal line with
, we proceed by approximating the extremal curve by a polygonal line with  segments and passing to the limit as the number of segments grows arbitrarily large.
segments and passing to the limit as the number of segments grows arbitrarily large.Divide the interval
![[a, b]](/2012-wikipedia_en_all_nopic_01_2012/I/2c3d331bc98b44e71cb2aae9edadca7e.png) into
into  equal segments with endpoints
equal segments with endpoints  and let
and let 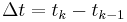 . Rather than a smooth function
. Rather than a smooth function 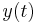 we consider the polygonal line with vertices
we consider the polygonal line with vertices 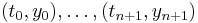 , where
, where 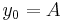 and
and 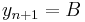 . Accordingly, our functional becomes a real function of
. Accordingly, our functional becomes a real function of  variables given by
variables given byExtremals of this new functional defined on the discrete points
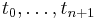 correspond to points where
correspond to points whereEvaluating this partial derivative gives
Dividing the above equation by
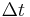 gives
givesand taking the limit as
 of the right-hand side of this expression yields
of the right-hand side of this expression yieldsThe left hand side of the previous equation is the functional derivative
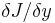 of the functional
of the functional  . A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
. A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
Examples
A standard example is finding the real-valued function on the interval [a, b], such that f(a) = c and f(b) = d, the length of whose graph is as short as possible. The length of the graph of f is:
the integrand function being L(x, y, y′) = √1 + y′ ² evaluated at (x, y, y′) = (x, f(x), f′(x)).
The partial derivatives of L are:
By substituting these into the Euler–Lagrange equation, we obtain
that is, the function must have constant first derivative, and thus its graph is a straight line.
Classical mechanics
Basic method
To find the equations of motions for a given system, one only has to follow these steps:
- From the kinetic energy
 , and the potential energy
, and the potential energy  , compute the Lagrangian
, compute the Lagrangian 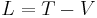 .
. - Compute
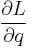 .
. - Compute
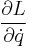 and from it,
and from it, 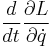 . It is important that
. It is important that 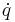 be treated as a complete variable in its own right, and not as a derivative.
be treated as a complete variable in its own right, and not as a derivative. - Equate
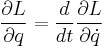 . This is the Euler–Lagrange equation.
. This is the Euler–Lagrange equation. - Solve the differential equation obtained in the preceding step. At this point,
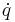 is treated "normally". Note that the above might be a system of equations and not simply one equation.
is treated "normally". Note that the above might be a system of equations and not simply one equation.
Particle in a conservative force field
The motion of a single particle in a conservative force field (for example, the gravitational force) can be determined by requiring the action to be stationary, by Hamilton's principle. The action for this system is
where x(t) is the position of the particle at time t. The dot above is Newton's notation for the time derivative: thus ẋ(t) is the particle velocity, v(t). In the equation above, L is the Lagrangian (the kinetic energy minus the potential energy):
where:
- m is the mass of the particle (assumed to be constant in classical physics);
- vi is the i-th component of the vector v in a Cartesian coordinate system (the same notation will be used for other vectors);
- U is the potential of the conservative force.
In this case, the Lagrangian does not vary with its first argument t. (By Noether's theorem, such symmetries of the system correspond to conservation laws. In particular, the invariance of the Lagrangian with respect to time implies the conservation of energy.)
By partial differentiation of the above Lagrangian, we find:
where the force is F = −∇U (the negative gradient of the potential, by definition of conservative force), and p is the momentum. By substituting these into the Euler–Lagrange equation, we obtain a system of second-order differential equations for the coordinates on the particle's trajectory,
which can be solved on the interval [t0, t1], given the boundary values xi(t0) and xi(t1). In vector notation, this system reads
or, using the momentum,
which is Newton's second law.
Variations for several functions, several variables, and higher derivatives
Single function of single variable with higher derivatives
The stationary values of the functional
can be obtained from the Euler–Lagrange equation[3]
Several functions of one variable
If the problem involves finding several functions ( ) of a single independent variable (
) of a single independent variable ( ) that define an extremum of the functional
) that define an extremum of the functional
then the corresponding Euler–Lagrange equations are[3]
Single function of several variables
A multi-dimensional generalization comes from considering a function on n variables. If Ω is some surface, then
is extremized only if f satisfies the partial differential equation
When n = 2 and 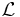 is the energy functional, this leads to the soap-film minimal surface problem.
is the energy functional, this leads to the soap-film minimal surface problem.
Several functions of several variables
If there are several unknown functions to be determined and several variables such that
the system of Euler–Lagrange equations is[3]
Single function of two variables with higher derivatives
If there is a single unknown function to be determined that is dependent on two variables and their higher derivatives such that
the Euler–Lagrange equation is[3]
Notes
References
- Weisstein, Eric W., "Euler-Lagrange Differential Equation" from MathWorld.
- Calculus of Variations on PlanetMath
- Izrail Moiseevich Gelfand (1963). Calculus of Variations. Dover. ISBN 0-486-41448-5.
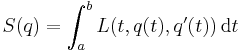
![\begin{align}
q \colon [a, b] \subset \mathbb{R} & \to X \\
t & \mapsto x = q(t)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/0163ce2c2f0a79b4da0cb9c704f03985.png)
![\begin{align}
q' \colon [a, b] & \to T_{q(t)}X \\
t & \mapsto v = q'(t)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6eacf3691f5c195a7be14edd1e08256a.png)
![\begin{align}
L \colon [a, b] \times X \times TX & \to \mathbb{R} \\
(t, x, v) & \mapsto L(t, x, v).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/f318638b3b55baa7d7d62b2a057151f4.png)
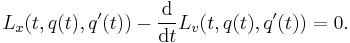
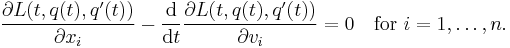
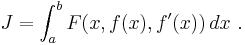
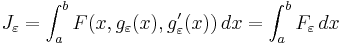
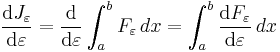
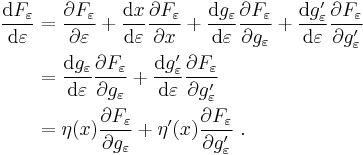
![\frac{\mathrm{d} J_\varepsilon}{\mathrm{d} \varepsilon} = \int_a^b \left[\eta(x) \frac{\partial F_\varepsilon}{\partial g_\varepsilon} %2B \eta'(x) \frac{\partial F_\varepsilon}{\partial g_\varepsilon'} \, \right]\,dx \ .](/2012-wikipedia_en_all_nopic_01_2012/I/2e59454f9a484b6c359d37460e3454ee.png)
![\frac{\mathrm d J_\varepsilon}{\mathrm d\varepsilon}\bigg|_{\varepsilon=0} = \int_a^b \left[ \eta(x) \frac{\partial F}{\partial f} %2B \eta'(x) \frac{\partial F}{\partial f'} \,\right]\,dx = 0 \ .](/2012-wikipedia_en_all_nopic_01_2012/I/2e903181c0f5a61f02a2a89b6550a554.png)
![\int_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx %2B \left[ \eta(x) \frac{\partial F}{\partial f'} \right]_a^b = 0 \ .](/2012-wikipedia_en_all_nopic_01_2012/I/32a174a856dcc8c4ba810b77a6993655.png)
![\int_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx = 0 \ . \,\!](/2012-wikipedia_en_all_nopic_01_2012/I/b0c29f201ee93c1c47520e00ab3b367a.png)
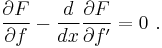
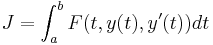
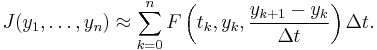
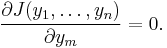
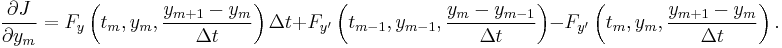
![\frac{\partial J}{\partial y_m \Delta t} = F_y\left(t_m, y_m, \frac{y_{m %2B 1} - y_m}{\Delta t}\right) - \frac{1}{\Delta t}\left[F_{y'}\left(t_m, y_m, \frac{y_{m %2B 1} - y_m}{\Delta t}\right) - F_{y'}\left(t_{m - 1}, y_{m - 1}, \frac{y_m - y_{m - 1}}{\Delta t}\right)\right],](/2012-wikipedia_en_all_nopic_01_2012/I/9f23d8e27c7fe3f2e39b37dc16150762.png)
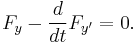
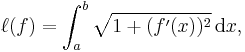
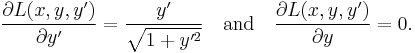
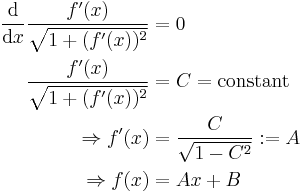
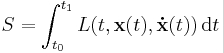
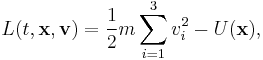
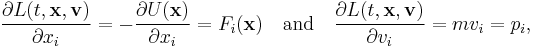
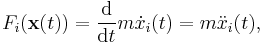
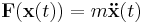
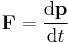
![I[f] = \int_{x_0}^{x_1} \mathcal{L}(x, f, f', f'', \dots, f^{(n)})~\mathrm{d}x ~;~~
f'�:= \cfrac{\mathrm{d}f}{\mathrm{d}x}, ~f''�:= \cfrac{\mathrm{d}^2f}{\mathrm{d}x^2}, ~
f^{(n)}�:= \cfrac{\mathrm{d}^nf}{\mathrm{d}x^n}](/2012-wikipedia_en_all_nopic_01_2012/I/a502eb7022b03884d406d6f5ef622df6.png)
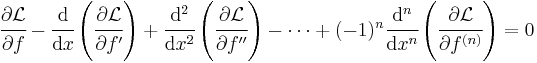
![I[f_1,f_2, \dots, f_n] = \int_{x_0}^{x_1} \mathcal{L}(x, f_1, f_2, \dots, f_n, f_1', f_2', \dots, f_n')~\mathrm{d}x
~;~~ f_i'�:= \cfrac{\mathrm{d}f_i}{\mathrm{d}x}](/2012-wikipedia_en_all_nopic_01_2012/I/fd54c9b17a87e46c0c24e2e1dc3db939.png)
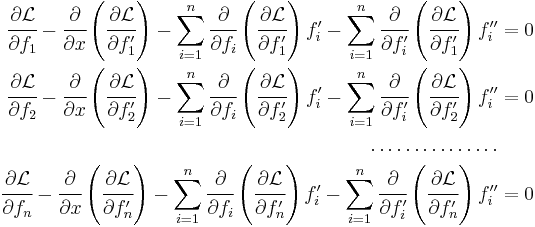
![I[f] = \int_{\Omega} \mathcal{L}(x_1, \dots , x_n, f, f_{x_1}, \dots , f_{x_n})\, \mathrm{d}\mathbf{x}\,\! ~;~~
f_{x_i}�:= \cfrac{\partial f}{\partial x_i}](/2012-wikipedia_en_all_nopic_01_2012/I/be771dae942a49056cbd7a514103b4b4.png)
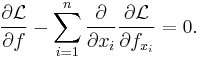
![I[f_1,f_2,\dots,f_m] = \int_{\Omega} \mathcal{L}(x_1, \dots , x_n, f_1, \dots, f_m, f_{1,1}, \dots , f_{1,n}, \dots, f_{m,1}, \dots, f_{m,n}) \, \mathrm{d}\mathbf{x}\,\! ~;~~
f_{j,i}�:= \cfrac{\partial f_j}{\partial x_i}](/2012-wikipedia_en_all_nopic_01_2012/I/4fe6b0cb4e2680092795c3f23f6970d7.png)
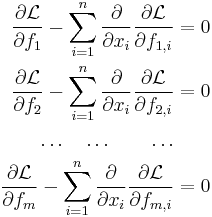
![\begin{align}
I[f] & = \int_{\Omega} \mathcal{L}(x_1, x_2, f, f_{,1}, f_{,2}, f_{,11}, f_{,12}, f_{,22},
\dots f_{,11\dots 1},\dots, f_{,1\dots 2})\, \mathrm{d}\mathbf{x}\,\! \\
& \qquad \quad
f_{,i}�:= \cfrac{\partial f}{\partial x_i} ~;~~ f_{,ij}�:= \cfrac{\partial^2 f}{\partial x_i\partial x_j} ~;~~
f_{,1\dots n}�:= \cfrac{\partial^{n} f}{\partial x_1\dots\partial x_n}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3c05ca1a08b45431aad578bfb22a9f9c.png)