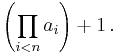Euclid–Mullin sequence
The Euclid–Mullin sequence is an infinite sequence of distinct prime numbers, in which each element is the least prime factor of one plus the product of all earlier elements. They are named after the ancient Greek mathematician Euclid, because their definition relies on an idea in Euclid's proof that there are infinitely many primes, and after Albert A. Mullin, who asked about the sequence in 1963.[1]
The first 47 elements of the sequence are
- 2, 3, 7, 43, 13, 53, 5, 6221671, 38709183810571, 139, 2801, 11, 17, 5471, 52662739, 23003, 30693651606209, 37, 1741, 1313797957, 887, 71, 7127, 109, 23, 97, 159227, 643679794963466223081509857, 103, 1079990819, 9539, 3143065813, 29, 3847, 89, 19, 577, 223, 139703, 457, 9649, 61, 4357, 87991098722552272708281251793312351581099392851768893748012603709343,[2] 107, 127, 3313, ... (sequence A000945 in OEIS)
These are the only known elements as of March 2010[update]. Finding the next one requires finding the least prime factor of a 256-digit number (which is known to be composite).
Contents |
Definition
If an denotes the n-th element of the sequence, then an is the least prime factor of
The first element is therefore the least prime factor of the empty product plus one, which is 2. The element 13 in the sequence is the least prime factor of 2 × 3 × 7 × 43 + 1 = 1806 + 1 = 1807 = 13 × 139.
Properties
The sequence is infinitely long and does not contain repeated elements. This can be proved using the method of Euclid's proof that there are infinitely many primes. That proof is constructive, and the sequence is the result of performing a version of that construction.
Conjecture
| Does every prime number appear in the Euclid–Mullin sequence? |
Mullin (1963) asked whether every prime number appears in the Euclid–Mullin sequence and, if not, whether the problem of testing a given prime for membership in the sequence is computable; these problems both remain open. The least prime number not known to be an element of the sequence is 31.
The positions of the prime numbers from 2 to 97 are:
- 1, 2, 7, 3, 12, 5, 13, 36, 25, 33, ?, 18, ?, 4, ?, 6, ?, 42, ?, 22, ?, ?, ?, 35, 26 (sequence A056756 in OEIS)
where ? indicates that the position (or whether it exists at all) is unknown as of 2008.[3]
Related sequences
A related sequence of numbers determined by the largest prime factor of one plus the product of the previous numbers (rather than the smallest prime factor) is also known as the Euclid–Mullin sequence. It grows more quickly, but is not monotonic.[4] The numbers in this sequence are
- 2, 3, 7, 43, 139, 50207, 340999, 2365347734339, 4680225641471129, 1368845206580129, 889340324577880670089824574922371, … (sequence A000946 in OEIS).
Alternatively, taking each number to be one plus the product of the previous numbers (rather than factoring it) gives Sylvester's sequence. The sequence constructed by repeatedly appending all factors of one plus the product of the previous numbers is the same as the sequence of prime factors of Sylvester's sequence. Like the Euclid–Mullin sequence, this is a non-monotonic sequence of primes, but it is known not to include all primes.[5]
See also
References
- ^ Mullin, Albert A. (1963), Recursive function theory (A modern look at a Euclidean idea), "Research problems", Bulletin of the American Mathematical Society 69 (6): 737, doi:10.1090/S0002-9904-1963-11017-4.
- ^ Factoring 43rd term of Euclid–Mullin sequence
- ^ The listing with the question marks is given in the Extensions field of the OEIS entry, whereas the main listing stops at 33 and has no question marks.
- ^ Naur, Thorkil (1984), "Mullin's sequence of primes is not monotonic", Proceedings of the American Mathematical Society 90 (1): 43–44, doi:10.2307/2044665, MR722412.
- ^ Guy, Richard; Nowakowski, Richard (1975), "Discovering primes with Euclid", Delta (Waukesha) 5 (2): 49–63, MR0384675.
External links
- Weisstein, Eric W., "Euclid–Mullin Sequence" from MathWorld.
- Factoring 43rd Term of Euclid–Mullin sequence, factorizations of the numbers for which the sequence elements is the smallest prime factor