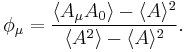Error analysis
Error analysis is the study of kind and quantity of error that occurs, particularly in the fields of applied mathematics (particularly numerical analysis), applied linguistics and statistics.
Contents |
Error analysis in numerical modeling
In numerical simulation or modeling of real systems, error analysis is concerned with the changes in the output of the model as the parameters to the model vary about a mean.
For instance, in a system modeled as a function of two variables 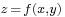 . Error analysis deals with the propagation of the numerical errors in
. Error analysis deals with the propagation of the numerical errors in  and
and  (around mean values
(around mean values 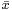 and
and 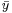 ) to error in
) to error in 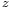 (around a mean
(around a mean 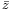 ).[1]
).[1]
In numerical analysis, error analysis comprises both forward error analysis and backward error analysis. Forward error analysis involves the analysis of a function 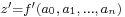 which is an approximation (usually a finite polynomial) to a function
which is an approximation (usually a finite polynomial) to a function 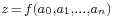 to determine the bounds on the error in the approximation; i.e., to find
to determine the bounds on the error in the approximation; i.e., to find 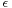 such that
such that 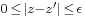 . Backward error analysis involves the analysis of the approximation function
. Backward error analysis involves the analysis of the approximation function 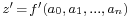 , to determine the bounds on the parameters
, to determine the bounds on the parameters 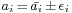 such that the result
such that the result 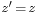 .[2]
.[2]
Error analysis in second language acquisition
In second language acquisition, error analysis studies the types and causes of language errors. Errors are classified[3] according to:
- modality (i.e., level of proficiency in speaking, writing, reading, listening)
- linguistic levels (i.e., pronunciation, grammar, vocabulary, style)
- form (e.g., omission, insertion, substitution)
- type (systematic errors/errors in competence vs. occasional errors/errors in performance)
- cause (e.g., interference, interlanguage)
- norm vs. system
Error analysis in SLA was established in the 1960s by Stephen Pit Corder and colleagues.[4] Error analysis was an alternative to contrastive analysis, an approach influenced by behaviorism through which applied linguists sought to use the formal distinctions between the learners' first and second languages to predict errors. Error analysis showed that contrastive analysis was unable to predict a great majority of errors, although its more valuable aspects have been incorporated into the study of language transfer. A key finding of error analysis has been that many learner errors are produced by learners making faulty inferences about the rules of the new language.
Error analysis in molecular dynamics simulation
In molecular dynamics (MD) simulations, there are errors due to inadequate sampling of the phase space or infrequently occurring events, these lead to the statistical error due to random fluctuation in the measurements.
For a series of M measurements of a fluctuating property A, the mean value is:
When these M measurements are independent, the variance of the mean <A> is:
but in most MD simulations, there is correlation between quantity A at different time, so the variance of the mean <A> will be underestimated as the effective number of independent measurements is actually less than M. In such situations we rewrite the variance as :
where 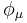 is the autocorrelation function defined by
is the autocorrelation function defined by
We can then use the autocorrelation function to estimate the error bar. Luckily, we have a much simpler method based on block averaging.[5]
See also
- Error bar
- Errors and residuals in statistics
- For error analysis in applied linguistics, see contrastive analysis
- Propagation of uncertainty
References
- ^ James W. Haefner (1996). Modeling Biological Systems: Principles and Applications. Springer. pp. 186–189. ISBN 0412042010.
- ^ Francis J. Scheid (1988). Schaum's Outline of Theory and Problems of Numerical Analysis. McGraw-Hill Professional. pp. 11. ISBN 0070552215.
- ^ Cf. Bussmann, Hadumod (1996), Routledge Dictionary of Language and Linguistics, London: Routledge, s.v. error analysis. A comprehensive bibliography was published by Bernd Spillner (1991), Error Analysis, Amsterdam/Philadelphia: Benjamins.
- ^ Corder, S. P. (1967). "The significance of learners' errors". International Review of Applied Linguistics 5: 160–170.
- ^ D. C. Rapaport, The Art of Molecular Dynamics Simulation, Cambridge University Press.
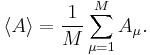
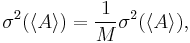
![\sigma^{2}( \langle A \rangle ) = \frac{1}{M} \sigma^{2}A \left[ 1 %2B 2 \sum_\mu \left( 1 - \frac{\mu}{M} \right) \phi_{\mu} \right],](/2012-wikipedia_en_all_nopic_01_2012/I/0e1603d7b9e6eb25a6e8c6da7762113c.png)