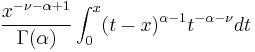Erdelyi–Kober operator

In mathematics, an Erdélyi–Kober operator is a fractional integration operation introduced by Arthur Erdélyi (1940) and Hermann Kober (1940).

The Erdélyi–Kober fractional integral is given by

$\frac{x^{-\nu-\alpha%2B1}}{\Gamma(\alpha)}\int_0^x (t-x)^{\alpha-1}t^{-\alpha-\nu} dt$

References

Erdélyi, A. (1940), "On fractional integration and its application to the theory of Hankel transforms", The Quarterly Journal of Mathematics. Oxford. Second Series 11: 293–303, doi:10.1093/qmath/os-11.1.293, ISSN 0033-5606, MR 0003271
Erdélyi, Arthur (1950–51), "On some functional transformations", Rendiconti del Seminario Matematico dell'Università e del Politecnico di Torino 10: 217–234, MR 0047818
Erdélyi, A.; Kober, H. (1940), "Some remarks on Hankel transforms", The Quarterly Journal of Mathematics. Oxford. Second Series 11: 212–221, doi:10.1093/qmath/os-11.1.212, ISSN 0033-5606, MR 0003270
Kober, Hermann (1940), "On fractional integrals and derivatives", The Quarterly Journal of Mathematics (Oxford Series) 11 (1): 193–211, doi:10.1093/qmath/os-11.1.193
Sneddon, Ian Naismith (1975), "The use in mathematical physics of Erdélyi-Kober operators and of some of their generalizations", in Ross, Bertram, Fractional calculus and its applications (Proc. Internat. Conf., Univ. New Haven, West Haven, Conn., 1974), Lecture Notes in Math., 457, Berlin, New York: Springer-Verlag, pp. 37–79, doi:10.1007/BFb0067097, ISBN 978-3-540-07161-7, MR 0487301