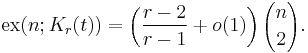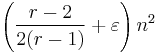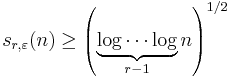Erdős–Stone theorem

In extremal graph theory, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem to bound the number of edges in an H-free graph for a non-complete graph H. It is named after Paul Erdős and Arthur Stone, who proved it in 1946,^[1] and it has been described as the “fundamental theorem of extremal graph theory”.^[2]

The extremal function ex(n; H) is defined to be the maximum number of edges in a graph of order n not containing a subgraph isomorphic to H. Turán's theorem says that ex(n; K_r) = t_r − 1(n), the order of the Turán graph, and that the Turán graph is the unique extremal graph. The Erdős-Stone theorem extends this to K_r(t), the complete t-partite graph with r vertices in each class, or equivalently the Turán graph T(rt,r):

An immediate corollary is that this applies to any graph H with chromatic number r, since such a graph is contained in K_r(t) for sufficiently large t but is not contained in any Turán graph T_r-1(n). For bipartite graphs H, however, the theorem gives only the limited information that ex(n; H) = o(n²), and for general bipartite graphs little more is known.

Quantitative results

Several versions of the theorem have been proved that more precisely characterise the relation of n, r, t and the o(1) term. Define the notation^[3] s_r,ε(n) (for 0 < ε < 1/(2(r − 1))) to be the greatest t such that every graph of order n and size

contains a K_r(t).

Erdős and Stone proved that

for n sufficiently large. The correct order of s_r,ε(n) in terms of n was found by Bollobás and Erdős^[4]: for any given r and ε there are constants c₁(r, ε) and c₂(r, ε) such that c₁(r, ε) log n < s_r,ε(n) < c₂(r, ε) log n. Chvátal and Szemerédi^[5] then determined the nature of the dependence on r and ε, up to a constant:

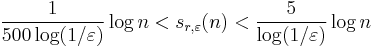for sufficiently large n.

Notes