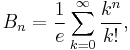Equivalence relation

This page is about a mathematical concept. For the patent doctrine, see Doctrine of equivalents.

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent (with respect to the equivalence relation) if and only if they are elements of the same cell. The intersection of any two cells is empty; the union of all the cells equals the original set.

Notation

Although various notations are used throughout the literature to denote that two elements a and b of a set are equivalent with respect to an equivalence relation R, the most common are "a ~ b" and "a ≡ b", which are used when R is the obvious relation being referenced, and variations of "a ~_R b", "a ≡_R b", or "aRb".

Definition

A given binary relation ~ on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive. Equivalently, for all a, b and c in A:

a ~ a. (Reflexivity)
if a ~ b then b ~ a. (Symmetry)
if a ~ b and b ~ c then a ~ c. (Transitivity)

A together with the relation ~ is called a setoid. The equivalence class of a under ~, denoted [a], is defined as $[a] = \{b\in A | a\sim b\}$ .

Reflexivity follows from symmetry and transitivity if for every element a∈A, there exists another element b∈A such that a~b holds. However, reflexivity does not follow from symmetry and transitivity alone. For example, let A be the set of integers, and let two elements of A be related if they are both even numbers. This relation is clearly symmetric and transitive, but in view of the existence of odd numbers, it is not reflexive.

On the other hand, let A be the set of integers, and let two elements of A be related if their difference is even. This is an equivalence relation, which partitions the integers into two equivalence classes, the even and odd integers.

Examples

Equivalence relations

The following are all equivalence relations:

"Is equal to" on the set of real numbers
"Has the same birthday as" on the set of all people.
"Is similar to" on the set of all triangles.
"Is congruent to" on the set of all triangles.
"Is congruent to, modulo n" on the integers.
"Has the same image under a function" on the elements of the domain of the function.
- "Has the same absolute value" on the set of real numbers
- "Has the same cosine" on the set of all angles.
"Is parallel to" on the set of subspaces of an affine space.

Relations that are not equivalences

The relation "≥" between real numbers is reflexive and transitive, but not symmetric. For example, 7 ≥ 5 does not imply that 5 ≥ 7. It is, however, a partial order.
The relation "has a common factor greater than 1 with" between natural numbers greater than 1, is reflexive and symmetric, but not transitive. (Example: The natural numbers 2 and 6 have a common factor greater than 1, and 6 and 3 have a common factor greater than 1, but 2 and 3 do not have a common factor greater than 1).
The empty relation R on a non-empty set X (i.e. aRb is never true) is vacuously symmetric and transitive, but not reflexive. (If X is also empty then R is reflexive.)
The relation "is approximately equal to" between real numbers, even if more precisely defined, is not an equivalence relation, because although reflexive and symmetric, it is not transitive, since multiple small changes can accumulate to become a big change. However, if the approximation is defined asymptotically, for example by saying that two functions f and g are approximately equal near some point if the limit of f-g is 0 at that point, then this defines an equivalence relation.
The relation "is a sibling of" (used to connote pairs of distinct people who have the same parents) on the set of all human beings is not an equivalence relation. Although siblinghood is symmetric (if A is a sibling of B, then B is a sibling of A) and transitive on any 3 distinct people (if A is a sibling of B and C is a sibling of B, then A is a sibling of C, provided A is not C), it is not reflexive (A cannot be a sibling of A).

Connections to other relations

A partial order is a relation that is reflexive, antisymmetric, and transitive.
A congruence relation is an equivalence relation whose domain X is also the underlying set for an algebraic structure, and which respects the additional structure. In general, congruence relations play the role of kernels of homomorphisms, and the quotient of a structure by a congruence relation can be formed. In many important cases congruence relations have an alternative representation as substructures of the structure on which they are defined. E.g. the congruence relations on groups correspond to the normal subgroups.
Equality is both an equivalence relation and a partial order. Equality is also the only relation on a set that is reflexive, symmetric and antisymmetric.
A strict partial order is irreflexive, transitive, and asymmetric.
A partial equivalence relation is transitive and symmetric. Transitive and symmetric imply reflexive if and only if for all a∈X, there exists a b∈X such that a~b.
A reflexive and symmetric relation is a dependency relation, if finite, and a tolerance relation if infinite.
A preorder is reflexive and transitive.

Well-definedness under an equivalence relation

If ~ is an equivalence relation on X, and P(x) is a property of elements of X, such that whenever x ~ y, P(x) is true if P(y) is true, then the property P is said to be well-defined or a class invariant under the relation ~.

A frequent particular case occurs when f is a function from X to another set Y; if x₁ ~ x₂ implies f(x₁) = f(x₂) then f is said to be a morphism for ~, a class invariant under ~, or simply invariant under ~. This occurs, e.g. in the character theory of finite groups. The latter case with the function f can be expressed by a commutative triangle. See also invariant. Some authors use "compatible with ~" or just "respects ~" instead of "invariant under ~".

More generally, a function may map equivalent arguments (under an equivalence relation ~_A) to equivalent values (under an equivalence relation ~_B). Such a function is known as a morphism from ~_A to ~_B.

Equivalence class, quotient set, partition

Let X be a nonempty set, and let 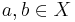$a,b\in X$ . Some definitions:

Equivalence class

Main article: Equivalence class

The set of all a and b for which a ~ b holds make up an equivalence class of X by ~. Let $[a]�:= \{x \in X | x \sim a\}$ denote the equivalence class to which a belongs. Then all elements of X equivalent to each other are also elements of the same equivalence class.

Quotient set

Main article: Quotient set

The set of all possible equivalence classes of X by ~, denoted $X/\sim�:= \{[x] | x \in X\}$ , is the quotient set of X by ~. If X is a topological space, there is a natural way of transforming X/~ into a topological space; see quotient space for the details.

Projection

Main article: Projection (relational algebra)

The projection of ~ is the function 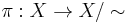$\pi: X \to X/\sim$ defined by $\pi(x) = [x]$ which maps elements of X into their respective equivalence classes by ~.

Theorem on projections:^[1] Let the function f: X → B be such that a ~ b → f(a) = f(b). Then there is a unique function g : X/~ → B, such that f = gπ. If f is a surjection and a ~ b ↔ f(a) = f(b), then g is a bijection.

Equivalence kernel

The equivalence kernel of a function f is the equivalence relation ~ defined by 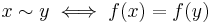$x\sim y \iff f(x) = f(y)$ . The equivalence kernel of an injection is the identity relation.

Partition

Main article: Partition of a set

A partition of X is a set P of nonempty subsets of X, such that every element of X is an element of a single element of P. Each element of P is a cell of the partition. Moreover, the elements of P are pairwise disjoint and their union is X.

Counting possible partitions

Let X be a finite set with n elements. Since every equivalence relation over X corresponds to a partition of X, and vice versa, the number of possible equivalence relations on X equals the number of distinct partitions of X, which is the nth Bell number B_n:

$B_n = \frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!},$

where the above is one of the ways to write the nth Bell number.

Fundamental theorem of equivalence relations

A key result links equivalence relations and partitions:^[2]^[3]

An equivalence relation ~ on a set X partitions X.
Conversely, corresponding to any partition of X, there exists an equivalence relation ~ on X.

In both cases, the cells of the partition of X are the equivalence classes of X by ~. Since each element of X belongs to a unique cell of any partition of X, and since each cell of the partition is identical to an equivalence class of X by ~, each element of X belongs to a unique equivalence class of X by ~. Thus there is a natural bijection from the set of all possible equivalence relations on X and the set of all partitions of X.

Comparing equivalence relations

If ~ and ≈ are two equivalence relations on the same set S, and a~b implies a≈b for all a,b ∈ S, then ≈ is said to be a coarser relation than ~, and ~ is a finer relation than ≈. Equivalently,

~ is finer than ≈ if every equivalence class of ~ is a subset of an equivalence class of ≈, and thus every equivalence class of ≈ is a union of equivalence classes of ~.
~ is finer than ≈ if the partition created by ~ is a refinement of the partition created by ≈.

The equality equivalence relation is the finest equivalence relation on any set, while the trivial relation that makes all pairs of elements related is the coarsest.

The relation "~ is finer than ≈" on the collection of all equivalence relations on a fixed set is itself a partial order relation.

Generating equivalence relations

Given any set X, there is an equivalence relation over the set [X→X] of all possible functions X→X. Two such functions are deemed equivalent when their respective sets of fixpoints have the same cardinality, corresponding to cycles of length one in a permutation. Functions equivalent in this manner form an equivalence class on [X→X], and these equivalence classes partition [X→X].

An equivalence relation ~ on X is the equivalence kernel of its surjective projection π : X → X/~.^[4] Conversely, any surjection between sets determines a partition on its domain, the set of preimages of singletons in the codomain. Thus an equivalence relation over X, a partition of X, and a projection whose domain is X, are three equivalent ways of specifying the same thing.

The intersection of any collection of equivalence relations over X (viewed as a subset of X × X) is also an equivalence relation. This yields a convenient way of generating an equivalence relation: given any binary relation R on X, the equivalence relation generated by R is the smallest equivalence relation containing R. Concretely, R generates the equivalence relation a ~ b if and only if there exist elements x₁, x₂, ..., x_n in X such that a = x₁, b = x_n, and (x_i,x_{i+ 1})∈R or (x_i+1,x_i)∈R, i = 1, ..., n-1.

Note that the equivalence relation generated in this manner can be trivial. For instance, the equivalence relation ~ generated by:

Any total order on X has exactly one equivalence class, X itself, because x ~ y for all x and y;
Any subset of the identity relation on X has equivalence classes that are the singletons of X.

Equivalence relations can construct new spaces by "gluing things together." Let X be the unit Cartesian square [0,1] × [0,1], and let ~ be the equivalence relation on X defined by ∀a, b ∈ [0,1] ((a, 0) ~ (a, 1) ∧ (0, b) ~ (1, b)). Then the quotient space X/~ can be naturally identified with a torus: take a square piece of paper, bend and glue together the upper and lower edge to form a cylinder, then bend the resulting cylinder so as to glue together its two open ends, resulting in a torus.

Algebraic structure

Much of mathematics is grounded in the study of equivalences, and order relations. lattice theory captures the mathematical structure of order relations. Even though equivalence relations are as ubiquitous in mathematics as order relations, the algebraic structure of equivalences is not as well known as that of orders. The former structure draws primarily on group theory and, to a lesser extent, on the theory of lattices, categories, and groupoids.

Group theory

Just as order relations are grounded in ordered sets, sets closed under pairwise supremum and infimum, equivalence relations are grounded in partitioned sets, which are sets closed under bijections and preserve partition structure. Since all such bijections map an equivalence class onto itself, such bijections are also known as permutations. Hence permutation groups (also known as transformation groups) and the related notion of orbit shed light on the mathematical structure of equivalence relations.

Let '~' denote an equivalence relation over some nonempty set A, called the universe or underlying set. Let G denote the set of bijective functions over A that preserve the partition structure of A: ∀x ∈ A ∀g ∈ G (g(x) ∈ [x]). Then the following three connected theorems hold:^[5]

~ partitions A into equivalence classes. (This is the Fundamental Theorem of Equivalence Relations, mentioned above);
Given a partition of A, G is a transformation group under composition, whose orbits are the cells of the partition‡;
Given a transformation group G over A, there exists an equivalence relation ~ over A, whose equivalence classes are the orbits of G.^[6]^[7]

In sum, given an equivalence relation ~ over A, there exists a transformation group G over A whose orbits are the equivalence classes of A under ~.

This transformation group characterisation of equivalence relations differs fundamentally from the way lattices characterize order relations. The arguments of the lattice theory operations meet and join are elements of some universe A. Meanwhile, the arguments of the transformation group operations composition and inverse are elements of a set of bijections, A → A.

Moving to groups in general, let H be a subgroup of some group G. Let ~ be an equivalence relation on G, such that a ~ b ↔ (ab⁻¹ ∈ H). The equivalence classes of ~—also called the orbits of the action of H on G—are the right cosets of H in G. Interchanging a and b yields the left cosets.

‡Proof.^[8] Let function composition interpret group multiplication, and function inverse interpret group inverse. Then G is a group under composition, meaning that ∀x ∈ A ∀g ∈ G ([g(x)] = [x]), because G satisfies the following four conditions:

G is closed under composition. The composition of any two elements of G exists, because the domain and codomain of any element of G is A. Moreover, the composition of bijections is bijective;^[9]
Existence of identity element. The identity function, I(x)=x, is an obvious element of G;
Existence of inverse function. Every bijective function g has an inverse g⁻¹, such that gg⁻¹ = I;
Composition associates. f(gh) = (fg)h. This holds for all functions over all domains.^[10]

Let f and g be any two elements of G. By virtue of the definition of G, [g(f(x))] = [f(x)] and [f(x)] = [x], so that [g(f(x))] = [x]. Hence G is also a transformation group (and an automorphism group) because function composition preserves the partitioning of A. $\square$

Related thinking can be found in Rosen (2008: chpt. 10).

Categories and groupoids

Let G be a set and let "~" denote an equivalence relation over G. Then we can form a groupoid representing this equivalence relation as follows. The objects are the elements of G, and for any two elements x and y of G, there exists a unique morphism from x to y if and only if x~y.

The advantages of regarding an equivalence relation as a special case of a groupoid include:

Whereas the notion of "free equivalence relation" does not exist, that of a free groupoid on a directed graph does. Thus it is meaningful to speak of a "presentation of an equivalence relation," i.e., a presentation of the corresponding groupoid;
Bundles of groups, group actions, sets, and equivalence relations can be regarded as special cases of the notion of groupoid, a point of view that suggests a number of analogies;
In many contexts "quotienting," and hence the appropriate equivalence relations often called congruences, are important. This leads to the notion of an internal groupoid in a category.^[11]

Lattices

The possible equivalence relations on any set X, when ordered by set inclusion, form a complete lattice, called Con X by convention. The canonical map ker: X^X → Con X, relates the monoid X^X of all functions on X and Con X. ker is surjective but not injective. Less formally, the equivalence relation ker on X, takes each function f: X→X to its kernel ker f. Likewise, ker(ker) is an equivalence relation on X^X.

Equivalence relations and mathematical logic

Equivalence relations are a ready source of examples or counterexamples. For example, an equivalence relation with exactly two infinite equivalence classes is an easy example of a theory which is ω-categorical, but not categorical for any larger cardinal number.

An implication of model theory is that the properties defining a relation can be proved independent of each other (and hence necessary parts of the definition) if and only if, for each property, examples can be found of relations not satisfying the given property while satisfying all the other properties. Hence the three defining properties of equivalence relations can be proved mutually independent by the following three examples:

Reflexive and transitive: The relation ≤ on N. Or any preorder;
Symmetric and transitive: The relation R on N, defined as aRb ↔ ab ≠ 0. Or any partial equivalence relation;
Reflexive and symmetric: The relation R on Z, defined as aRb ↔ "a − b is divisible by at least one of 2 or 3." Or any dependency relation.

Properties definable in first-order logic that an equivalence relation may or may not possess include:

The number of equivalence classes is finite or infinite;
The number of equivalence classes equals the (finite) natural number n;
All equivalence classes have infinite cardinality;
The number of elements in each equivalence class is the natural number n.

Euclidean relations

Euclid's The Elements includes the following "Common Notion 1":

Things which equal the same thing also equal one another.

Nowadays, the property described by Common Notion 1 is called Euclidean (replacing "equal" by "are in relation with"). The following theorem connects Euclidean relations and equivalence relations:

Theorem. If a relation is Euclidean and reflexive, it is also symmetric and transitive.

Proof:

(aRc ∧ bRc) → aRb [a/c] = (aRa ∧ bRa) → aRb [reflexive; erase T∧] = bRa → aRb. Hence R is symmetric.
(aRc ∧ bRc) → aRb [symmetry] = (aRc ∧ cRb) → aRb. Hence R is transitive. $\square$

Hence an equivalence relation is a relation that is Euclidean and reflexive. The Elements mentions neither symmetry nor reflexivity, and Euclid probably would have deemed the reflexivity of equality too obvious to warrant explicit mention.

Notes

^ Garrett Birkhoff and Saunders Mac Lane, 1999 (1967). Algebra, 3rd ed. p. 35, Th. 19. Chelsea.
^ Wallace, D. A. R., 1998. Groups, Rings and Fields. p. 31, Th. 8. Springer-Verlag.
^ Dummit, D. S., and Foote, R. M., 2004. Abstract Algebra, 3rd ed. p. 3, Prop. 2. John Wiley & Sons.
^ Garrett Birkhoff and Saunders Mac Lane, 1999 (1967). Algebra, 3rd ed. p. 33, Th. 18. Chelsea.
^ Rosen (2008), pp. 243-45. Less clear is §10.3 of Bas van Fraassen, 1989. Laws and Symmetry. Oxford Univ. Press.
^ Wallace, D. A. R., 1998. Groups, Rings and Fields. Springer-Verlag: 202, Th. 6.
^ Dummit, D. S., and Foote, R. M., 2004. Abstract Algebra, 3rd ed. John Wiley & Sons: 114, Prop. 2.
^ Bas van Fraassen, 1989. Laws and Symmetry. Oxford Univ. Press: 246.
^ Wallace, D. A. R., 1998. Groups, Rings and Fields. Springer-Verlag: 22, Th. 6.
^ Wallace, D. A. R., 1998. Groups, Rings and Fields. Springer-Verlag: 24, Th. 7.
^ Borceux, F. and Janelidze, G., 2001. Galois theories, Cambridge University Press, ISBN 0-521-80309-8

References

Brown, Ronald, 2006. Topology and Groupoids. Booksurge LLC. ISBN 1419627228.
Castellani, E., 2003, "Symmetry and equivalence" in Brading, Katherine, and E. Castellani, eds., Symmetries in Physics: Philosophical Reflections. Cambridge Univ. Press: 422-433.
Robert Dilworth and Crawley, Peter, 1973. Algebraic Theory of Lattices. Prentice Hall. Chpt. 12 discusses how equivalence relations arise in lattice theory.
Higgins, P.J., 1971. Categories and groupoids. Van Nostrand. Downloadable since 2005 as a TAC Reprint.
John Randolph Lucas, 1973. A Treatise on Time and Space. London: Methuen. Section 31.
Rosen, Joseph (2008) Symmetry Rules: How Science and Nature are Founded on Symmetry. Springer-Verlag. Mostly chpts. 9,10.

External links

Bogomolny, A., "Equivalence Relationship" cut-the-knot. Accessed 1 September 2009
Equivalence relation at PlanetMath