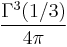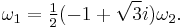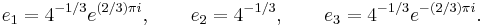Equianharmonic

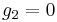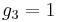In mathematics, and in particular the study of Weierstrass elliptic functions, the equianharmonic case occurs when the Weierstrass invariants satisfy $g_2=0$ and $g_3=1$ ; This page follows the terminology of Abramowitz and Stegun; see also the lemniscatic case. (These are special examples of complex multiplication).

In the equianharmonic case, the minimal half period 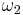$\omega_2$ is real and equal to

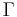$\frac{\Gamma^3(1/3)}{4\pi}$

where $\Gamma$ is the Gamma function. The half period is

$\omega_1=\tfrac{1}{2}(-1%2B\sqrt3i)\omega_2.$

Here the period lattice is a real multiple of the Eisenstein integers.

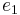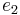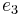The constants $e_1$ , $e_2$ and $e_3$ are given by

$e_1=4^{-1/3}e^{(2/3)\pi i},\qquad e_2=4^{-1/3},\qquad e_3=4^{-1/3}e^{-(2/3)\pi i}.$

The case g₂=0, g₃=a may be handled by a scaling transformation.