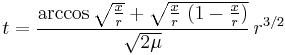Equations for a falling body
Under normal earth-bound conditions, when objects move owing to a constant gravitational force a set of dynamical equations describe the resultant trajectories. For example, Newton's law of universal gravitation simplifies to F = mg, where m is the mass of the body. This assumption is reasonable for objects falling to earth over the relatively short vertical distances of our everyday experience, but is very much untrue over larger distances, such as spacecraft trajectories. Please note that in this article any resistance from air (drag) is neglected.
Contents |
History
Galileo was the first to demonstrate and then formulate these equations. He used a ramp to study rolling balls, the ramp slowing the acceleration enough to measure the time taken for the ball to roll a known distance. He measured elapsed time with a water clock, using an "extremely accurate balance" to measure the amount of water.[note 1]
The equations ignore air resistance, which has a dramatic effect on objects falling an appreciable distance in air, causing them to quickly approach a terminal velocity. The effect of air resistance varies enormously depending on the size and geometry of the falling object — for example, the equations are hopelessly wrong for a feather, which has a low mass but offers a large resistance to the air. (In the absence of an atmosphere all objects fall at the same rate, as astronaut David Scott demonstrated by dropping a hammer and a feather on the surface of the Moon.)
The equations also ignore the rotation of the Earth, failing to describe the Coriolis effect for example. Nevertheless, they are usually accurate enough for dense and compact objects falling over heights not exceeding the tallest man-made structures.
Overview
Near the surface of the Earth, use g = 9.8 m/s² (metres per second squared; which might be thought of as "metres per second, per second", or 32 ft/s² as "feet per second per second"), approximately. For other planets, multiply g by the appropriate scaling factor. It is essential to use a coherent set of units for g, d, t and v. Assuming SI units, g is measured in metres per second squared, so d must be measured in metres, t in seconds and v in metres per second.
In all cases the body is assumed to start from rest, and air resistance is neglected. Generally, in Earth's atmosphere, this means all results below will be quite inaccurate after only 5 seconds of fall (at which time an object's velocity will be a little less than the vacuum value of 49 m/s (9.8 m/s² × 5 s), due to air resistance). For a body encountering a thick atmosphere like the Earth's near sea level, terminal velocity is reached exponentially between 8 and 15 seconds, after which a steady velocity of very approximately 100 m/s is maintained for compact objects with densities between those of water and common metals.
On an airless body like the moon or relatively airless body like Mars, with appropriate changes in g, these equations will yield accurate results over much longer times and much higher velocities.
Apart from the last formula, these formulas also assume that g does not vary significantly with height during the fall (that is, they assume constant acceleration). For situations where fractional distance from the center of the planet varies significantly during the fall, resulting in significant changes in g, the last equation must be used for accuracy.
Distance 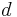 travelled by an object falling for time travelled by an object falling for time 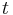 : : |
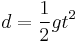 |
Time 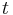 taken for an object to fall distance taken for an object to fall distance 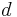 : : |
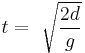 |
Instantaneous velocity 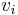 of a falling object after elapsed time of a falling object after elapsed time 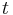 : : |
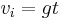 |
Instantaneous velocity 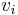 of a falling object that has travelled distance of a falling object that has travelled distance 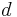 : : |
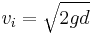 |
Average velocity 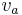 of an object that has been falling for time of an object that has been falling for time 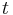 (averaged over time): (averaged over time): |
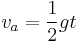 |
Average velocity 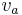 of a falling object that has travelled distance of a falling object that has travelled distance 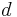 (averaged over time): (averaged over time): |
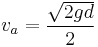 |
Instantaneous velocity 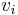 of a falling object that has travelled distance of a falling object that has travelled distance 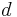 on a planet with mass on a planet with mass 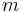 , with the combined radius of the planet and altitude of the falling object being , with the combined radius of the planet and altitude of the falling object being 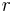 , this equation is used for larger radii where , this equation is used for larger radii where 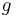 is smaller than standard is smaller than standard 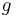 at the surface of Earth, but assumes a small distance of fall, so the change in at the surface of Earth, but assumes a small distance of fall, so the change in 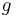 is small and relatively constant: is small and relatively constant: |
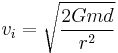 |
Instantaneous velocity 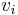 of a falling object that has travelled distance of a falling object that has travelled distance 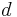 on a planet with mass on a planet with mass 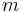 and radius and radius 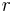 (used for large fall distances where (used for large fall distances where 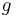 can change significantly): can change significantly): |
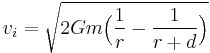 |
Example: the first equation shows that, after one second, an object will have fallen a distance of 1/2 × 9.8 × 12 = 4.9 meters. After two seconds it will have fallen 1/2 × 9.8 × 22 = 19.6 metres; and so on.
We can see how the second to last, and the last equation change as the distance increases. If an object were to fall 10,000 meters to Earth, the results of both equations differ by only 0.08%. However, if the distance increases to that of geosynchronous orbit, which is 42,164 km, the difference changes to being almost 64%. At high values, the results of the second to last equation become grossly inaccurate.
For astronomical bodies other than Earth, and for short distances of fall at other than "ground" level, g in the above equations may be replaced by G(M+m)/r² where G is the gravitational constant, M is the mass of the astronomical body, m is the mass of the falling body, and r is the radius from the falling object to the center of the body.
Removing the simplifying assumption of uniform gravitational acceleration provides more accurate results. We find from the formula for radial elliptic trajectories:
The time t taken for an object to fall from a height r to a height x, measured from the centers of the two bodies, is given by:
where 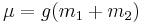 is the sum of the standard gravitational parameters of the two bodies. This equation should be used whenever there is a significant difference in the gravitational acceleration during the fall.
is the sum of the standard gravitational parameters of the two bodies. This equation should be used whenever there is a significant difference in the gravitational acceleration during the fall.
Acceleration relative to the rotating Earth
The acceleration measured on the rotating surface of the Earth is not quite the same as the acceleration that is measured for a free-falling body because of the centripetal force. In other words, the apparent acceleration in the rotating frame of reference is the total gravity vector minus a small vector toward the north-south axis of the Earth, corresponding to staying stationary in that frame of reference.
See also
Notes
- ^ See the works of Stillman Drake, for a comprehensive study of Galileo and his times, the Scientific Revolution.