Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for every note in the system.
In equal temperament tunings, an interval — usually the octave — is divided into a series of equal steps (equal frequency ratios between successive notes). For classical music, the most common tuning system is twelve-tone equal temperament (also known as 12 equal temperament), inconsistently abbreviated as 12-TET, 12TET, 12tET, 12tet, 12-ET, 12ET, or 12et, which divides the octave into 12 parts, all of which are equal on a logarithmic scale. It is usually tuned relative to a standard pitch of 440 Hz, called A 440.
Other equal temperaments exist (some music has been written in 19-TET and 31-TET for example, and 24-TET) 24-TET is used in Arabic music, but in western countries when people use the term equal temperament without qualification, it is usually understood that they are talking about 12-TET.
Equal temperaments may also divide some interval other than the octave, a pseudo-octave, into a whole number of equal steps. An example is an equal-tempered Bohlen–Pierce scale. To avoid ambiguity, the term equal division of the octave, or EDO is sometimes preferred. According to this naming system, 12-TET is called 12-EDO, 31-TET is called 31-EDO, and so on.
String ensembles and vocal groups, who have no mechanical tuning limitations, often use a tuning much closer to just intonation, as it is naturally more consonant. Other instruments, such as some wind, keyboard, and fretted instruments, often only approximate equal temperament, where technical limitations prevent exact tunings. Other wind instruments, that can easily and spontaneously bend their tone, most notably double-reeds, use tuning similar to string ensembles and vocal groups.
Contents |
Equal temperament in Europe
Early history
One of the earliest discussions of equal temperament occurs in the writiting of Aristoxenus in the 4th century B.C.
Vincenzo Galilei (father of Galileo Galilei) was one of the first practical advocates of twelve-tone equal temperament. He composed a set of dance suites on each of the 12 notes of the chromatic scale in all the "transposition keys", and published also, in his 1584 "Fronimo", 24 +1 ricercars.[1] He used the 18:17 ratio for fretting the lute (although some adjustment was necessary for pure octaves).[2]
Galilei's countryman and fellow lutenist Giacomo Gorzanis had written music based on equal temperament by 1567.[3][4] Gorzanis was not the only lutenist to explore all modes or keys: Francesco Spinacino wrote a "Recercare de tutti li Toni" as early as 1507.[5] In the 17th century lutenist-composer John Wilson wrote a set of 30 preludes including 24 in all the major/minor keys.[6][7]
Henricus Grammateus drew a close approximation to equal temperament in 1518. The first tuning rules in equal temperament were given by Giovani Maria Lanfranco in his "Scintille de musica".[8]
- Simon Stevin
The first mention of equal temperament related to Twelfth root of two in the West appeared in Simon Stevin's manuscript Van De Spiegheling der signconst (ca 1605) published posthumously nearly three centuries later in 1884[9]. However, due to insufficient accuracy of his calculation, many of the chord length numbers he obtained were off by one or two units from the correct values[10]. As a result, the frequency ratios of Simon Stevin's chords has no unified ratio, but one ratio per tone, which is claimed by Gene Cho as incorrect[11].
The following were Simon Stevin's chord length from Vande Spiegheling der signconst:[12]
| TONE | CHORD 10000 from Simon Stevin | RATIO | CORRECTED CHORD |
|---|---|---|---|
| semitone | 9438 | 1.0595465 | 9438.7 |
| whole tone | 8909 | 1.0593781 | |
| 1.5 tone | 8404 | 1.0600904 | 8409 |
| ditone | 7936 | 1.0594758 | 7937 |
| ditone and a half | 7491 | 1.0594046 | 7491.5 |
| tritone | 7071 | 1.0593975 | 7071.1 |
| tritone and a half | 6674 | 1.0594845 | 6674.2 |
| four-tone | 6298 | 1.0597014 | 6299 |
| four-tone-and-half | 5944 | 1.0595558 | 5946 |
| five-tone | 5611 | 1.0593477 | 5612.3 |
| five-tone-and-half | 5296 | 1.0594788 | 5297.2 |
| full tone | 1.0592000 |
A generation later, French mathematician Marin Mersenne presented several equal tempered chord lengths obtained by Jean Beaugrand, Ismael Bouillaud and Jean Galle.[13]
In 1630 Johann Faulhaber published a 100 cent monochord table, with the exception of several errors due to his use of logarithmic tables . He did not explain how he obtained his results.[14]
Zarlino in his polemic with Galilei initially opposed equal temperament but eventually conceded to it in relation to the lute in his "Sopplimenti musicali" in 1588.
Equal temperament in the Baroque era
From 1450 to about 1800 plucked instrument players (lutenists and guitarists) generally favored equal temperament[15], and the Brossard lute Manuscript compiled in the last quarter of the 17th century contains a series of 18 preludes attributed to Bocquet written in a all keys, including the last prelude, entitled "Prelude sur tous les tons", which enharmonically modulates through all of the keys. [16] Wind and keyboard musicians expected much less mistuning (than that of equal temperament) in the most common keys, such as C major. They used approximations that emphasized the tuning of thirds or fifths in these keys, such as meantone temperament. Among the 17th century keyboard composers Girolamo Frescobaldi advocated equal temperament. Some theorists, such as Giuseppe Tartini, were opposed to the adoption of equal temperament; they felt that degrading the purity of each chord degraded the aesthetic appeal of music, although Andreas Werckmeister emphatically advocated equal temperament in his 1707 treatise published posthumously.
J. S. Bach wrote The Well-Tempered Clavier to demonstrate the musical possibilities of well temperament, where in some keys the consonances are even more degraded than in equal temperament. It is reasonable to believe that when composers and theoreticians of earlier times wrote of the moods and "colors" of the keys, they each described the subtly different dissonances made available within a particular tuning method. However, it is difficult to determine with any exactness the actual tunings used in different places at different times by any composer. (Correspondingly, there is a great deal of variety in the particular opinions of composers about the moods and colors of particular keys.)
Twelve tone equal temperament took hold for a variety of reasons. It conveniently fit the existing keyboard design, and permitted total harmonic freedom at the expense of just a little impurity in every interval. This allowed greater expression through enharmonic modulation, which became extremely important in the 18th century in music of such composers as Francesco Geminiani, Wilhelm Friedemann Bach, Carl Philipp Emmanuel Bach and Johann Gottfried Müthel.
The progress of Equal Temperament from mid-18th century on is described with detail in quite a few modern scholarly publications: it was already the temperament of choice during the Classical era (second half of the 18th century), and it became standard during the Early Romantic era (first decade of the 19th century), except for organs that switched to it more gradually, completing only in the second decade of the 19th century. (In England, some cathedral organists and choirmasters held out against it even after that date; Samuel Sebastian Wesley, for instance, opposed it all along. He died in 1876.)
A precise equal temperament is possible using the 17th-century Sabbatini method of splitting the octave first into three tempered major thirds. This was also proposed by several writers during the Classical era. Tuning with several checks, thus attaining virtually modern accuracy, was already done in the 1st decades of the 19th century. Using beat rates, first proposed in 1749, became common after their diffusion by Helmholtz and Ellis in the second half of the 19th century. The ultimate precision was available with 2-decimal tables published by White in 1917.
It is in the environment of equal temperament that the new styles of symmetrical tonality and polytonality, atonal music such as that written with the twelve tone technique or serialism, and jazz (at least its piano component) developed and flourished.
Equal temperament in China
The earliest discussion of the equal division of the scale was in the writings of Ling Lun during the 27th century BC.[17]
Jing Fang (78–37 BC) observed that using the Pythagorean comma of 53 just fifths approximates to 31 octaves. This would later lead to the discovery of 53 equal temperament.
An approximation for equal temperament was given by He Chengtian, a mathematician of Southern and Northern Dynasties around 400 AD.[18]
Historically, there was a seven-equal temperament or hepta-equal temperament practice in Chinese tradition.[19][20]
Zhu Zaiyu (朱載堉), a prince of the Ming court, spent thirty years on research based on the equal temperament idea originally postulated by his father. He described his new pitch theory in his Fusion of Music and Calendar 乐律融通 published in 1580. This was followed by the publication of a detailed account of the new theory of the equal temperament with a precise numerical specification for 12-TET in his five thousand pages work Complete Compendium of Music and Pitch(Yuelü quan shu 乐律全书) in 1584.[21]
He obtained his result mathematically by dividing the length of string and pipe successively by
![\sqrt [12]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/70b8b8fc763c20423a65bd934e378085.png) =1.059463094359295264561825, and for pipe diameter by
=1.059463094359295264561825, and for pipe diameter by
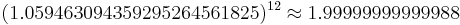
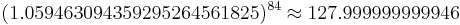 (after 8 octave still in tune)
(after 8 octave still in tune)
According to Gene Cho, Zhu Zaiyu was the first person to solve equal temperament problem mathematically.[23][24] Murray Bardour said, "The first known appearance in print of the correct figures for equal temperament was in China, where Prince Tsaiyii's brilliant solution remains an enigma."[25] The 19th-century German physicist Hermann von Helmholtz wrote in On the Sensations of Tone that a Chinese prince (see below) introduced a scale of seven notes, and that the division of the octave into twelve semitones was discovered in China.[26]
Zhu Zaiyu tuning instrument
Zhu Zaiyu illustrated his equal temperament theory by construction of a set of 36 bamboo tuning pipes ranging in 3 octaves, with instructions of the type of bamboo, color of paint, and detailed specification on their length and inner and outer diameters. He also constructed a 12-string tuning instrument, with a set of tuning pitch pipes hidden inside its bottom cavity. In 1890, Victor-Charles Mahillon, curator of the Conservatoire museum in Brussels, duplicated a set of pitch pipes according to Zhu Zaiyu's specification. He said that the Chinese theory of tones knew more about the diameter of pitch pipes than its Western counterpart, and that the set of pipes duplicated according to the Zaiyu data proved the accuracy of this theory.[27].
General properties
In an equal temperament, the distance between each step of the scale is the same interval. Because the perceived identity of an interval depends on its ratio, this scale in even steps is a geometric sequence of multiplications. (An arithmetic sequence of intervals would not sound evenly-spaced, and would not permit transposition to different keys.) Specifically, the smallest interval in an equal-tempered scale is the ratio:
where the ratio r divides the ratio p (typically the octave, which is 2/1) into n equal parts. (See Twelve-tone equal temperament below.)
Scales are often measured in cents, which divide the octave into 1200 equal intervals (each called a cent). This logarithmic scale makes comparison of different tuning systems easier than comparing ratios, and has considerable use in Ethnomusicology. The basic step in cents for any equal temperament can be found by taking the width of p above in cents (usually the octave, which is 1200 cents wide), called below w, and dividing it into n parts:
In musical analysis, material belonging to an equal temperament is often given an integer notation, meaning a single integer is used to represent each pitch. This simplifies and generalizes discussion of pitch material within the temperament in the same way that taking the logarithm of a multiplication reduces it to addition. Furthermore, by applying the modular arithmetic where the modulo is the number of divisions of the octave (usually 12), these integers can be reduced to pitch classes, which removes the distinction (or acknowledges the similarity) between pitches of the same name, e.g. 'C' is 0 regardless of octave register. The MIDI encoding standard uses integer note designations.
Twelve-tone equal temperament
In twelve-tone equal temperament, which divides the octave into 12 equal parts, the width of a semitone, i.e. the frequency ratio of the interval between two adjacent notes, is the twelfth root of two:
![\sqrt[12]{2}=2^{\frac{1}{12}}\approx 1.059463094359295264561825294946](/2012-wikipedia_en_all_nopic_01_2012/I/c52b6cef8aba82b04915a7e4afc7cd58.png)
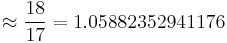 (98.9545922303676 CENT)
(98.9545922303676 CENT)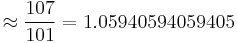 (99.9066043792227 CENT)
(99.9066043792227 CENT)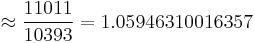 (100.0000094845790 CENT)
(100.0000094845790 CENT)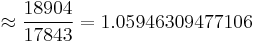 (100.0000006728490 CENT)
(100.0000006728490 CENT)
This interval is divided into 100 cents. (The cent is sometimes for this reason defined as one hundredth of a semitone.)
Calculating absolute frequencies
To find the frequency, Pn, of a note in 12-TET, the following definition may be used:
In this formula Pn refers to the pitch, or frequency (usually in hertz), you are trying to find. Pa refers to the frequency of a reference pitch (usually 440Hz). n and a refer to numbers assigned to the desired pitch and the reference pitch, respectively. These two numbers are from a list of consecutive integers assigned to consecutive semitones. For example, A4 (the reference pitch) is the 49th key from the left end of a piano (tuned to 440 Hz), and C4 (middle C) is the 40th key. These numbers can be used to find the frequency of C4:
Comparison of various equal temperament in history
| YEAR | NAME | RATIO | CENTS |
|---|---|---|---|
| 400 | He Chengtian | 1.060070671 | 101.0 |
| 1580 | Vincenzo Galilei | 18:17 | 99.0 |
| 1581 | Zhu Zaiyu | 1.059463094 | 100.0 |
| 1585 | Simon Stevin | 1.059546514 | 100.1 |
| 1630 | Marin Mersenne | 1.059322034 | 99.8 |
| 1630 | Johann Faulhaber | 1.059490385 | 100.0 |
Comparison to just intonation
The intervals of 12-TET closely approximate some intervals in just intonation. The fifths and fourths are almost indistinguishably close to just.
In the following table the sizes of various just intervals are compared against their equal-tempered counterparts, given as a ratio as well as cents.
| Name | Exact value in 12-TET | Decimal value in 12-TET | Cents | Just intonation interval | Cents in just intonation | Error |
|---|---|---|---|---|---|---|
| Unison (C) |  |
1.000000 | 0 |  = 1.000000 = 1.000000 |
0.00 | 0 |
| Minor second (C♯/D♭) | ![2^{1/12} = \sqrt[12]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/1c323b6c1d805e260ba1ebafe180decf.png) |
1.059463 | 100 | 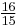 = 1.066667 = 1.066667 |
111.73 | −11.73 |
| Major second (D) | ![2^{2/12} = \sqrt[6]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/a28f7edb1a398ffab8f42ac9b16dfd8d.png) |
1.122462 | 200 | 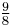 = 1.125000 = 1.125000 |
203.91 | −3.91 |
| Minor third (D♯/E♭) | ![2^{3/12} = \sqrt[4]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/36e9f319b0ea5afe47b729f08e4ad532.png) |
1.189207 | 300 | 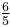 = 1.200000 = 1.200000 |
315.64 | −15.64 |
| Major third (E) | ![2^{4/12} = \sqrt[3]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/e077f20b356a38023c48f7352a304c08.png) |
1.259921 | 400 | 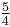 = 1.250000 = 1.250000 |
386.31 | +13.69 |
| Perfect fourth (F) | ![2^{5/12} = \sqrt[12]{32}](/2012-wikipedia_en_all_nopic_01_2012/I/f3742e11ac225b783a4daa0c1a8350e6.png) |
1.334840 | 500 | 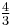 = 1.333333 = 1.333333 |
498.04 | +1.96 |
| Augmented fourth (F♯/G♭) | 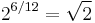 |
1.414214 | 600 | 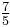 = 1.400000 = 1.400000 |
582.51 | +17.49 |
| Perfect fifth (G) | ![2^{7/12} = \sqrt[12]{128}](/2012-wikipedia_en_all_nopic_01_2012/I/48061b5c0376c5977de2aba65b1f986d.png) |
1.498307 | 700 | 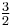 = 1.500000 = 1.500000 |
701.96 | −1.96 |
| Minor sixth (G♯/A♭) | ![2^{8/12} = \sqrt[3]{4}](/2012-wikipedia_en_all_nopic_01_2012/I/f52814ec9e29d7611585d9bcd3f893fd.png) |
1.587401 | 800 | 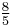 = 1.600000 = 1.600000 |
813.69 | −13.69 |
| Major sixth (A) | ![2^{9/12} = \sqrt[4]{8}](/2012-wikipedia_en_all_nopic_01_2012/I/85ca2708d0878b8858d1a7678c4b87a5.png) |
1.681793 | 900 | 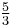 = 1.666667 = 1.666667 |
884.36 | +15.64 |
| Minor seventh (A♯/B♭) | ![2^{10/12} = \sqrt[6]{32}](/2012-wikipedia_en_all_nopic_01_2012/I/177729758c064ee402d3f2dd50fb65a8.png) |
1.781797 | 1000 | 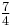 = 1.750000 = 1.750000 |
968.83 | +31.17 |
| Major seventh (B) | ![2^{11/12} = \sqrt[12]{2048}](/2012-wikipedia_en_all_nopic_01_2012/I/b78c388897c48d34f37d2ae727434d6d.png) |
1.887749 | 1100 | 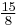 = 1.875000 = 1.875000 |
1088.27 | +11.73 |
| Octave (C) | 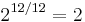 |
2.000000 | 1200 | 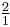 = 2.000000 = 2.000000 |
1200.00 | 0 |
Seven-tone equal division of the fifth
Violins, violas and cellos are tuned in perfect fifths (G - D - A - E, for violins, and C - G - D - A, for violas and cellos), which suggests that their semi-tone ratio will be slightly higher than in the conventional Twelve-tone Equal Temperament. Because a perfect fifth is in 3:2 relation with its base tone, and this interval is covered in 7 steps, each tone is in the ratio of ![\sqrt[7]{3/2}](/2012-wikipedia_en_all_nopic_01_2012/I/eefb97e88acba20ff2217a06ae18032a.png) to the next, which provides for a perfect fifth with ratio of 3:2 but a slightly widened octave with ratio of ≈ 517:258 or ≈ 2.00388:1 rather than the usual 2:1 ratio.[29] During actual play, however, the violinist chooses his pitches by ear, and only the four unstopped pitches of the strings are guaranteed to exhibit this 3:2 ratio.
to the next, which provides for a perfect fifth with ratio of 3:2 but a slightly widened octave with ratio of ≈ 517:258 or ≈ 2.00388:1 rather than the usual 2:1 ratio.[29] During actual play, however, the violinist chooses his pitches by ear, and only the four unstopped pitches of the strings are guaranteed to exhibit this 3:2 ratio.
Other equal temperaments
5 and 7 tone temperaments in ethnomusicology
Five and seven tone equal temperament (5-TET and 7-TET ), with 240 and 171 cent steps respectively, are fairly common. A Thai xylophone measured by Morton (1974) "varied only plus or minus 5 cents," from 7-TET. A Ugandan Chopi xylophone measured by Haddon (1952) was also tuned to this system. Indonesian gamelans are tuned to 5-TET according to Kunst (1949), but according to Hood (1966) and McPhee (1966) their tuning varies widely, and according to Tenzer (2000) they contain stretched octaves. It is now well-accepted that of the two primary tuning systems in gamelan music, slendro and pelog, only slendro somewhat resembles five-tone equal temperament while pelog is highly unequal; however, Surjodiningrat et al. (1972) has analyzed pelog as a seven-note subset of nine-tone equal temperament (133 cent steps ). A South American Indian scale from a preinstrumental culture measured by Boiles (1969) featured 175 cent seven tone equal temperament, which stretches the octave slightly as with instrumental gamelan music.
Various Western equal temperaments
31 tone equal temperament there advocated by Christiaan Huygens and Adriaan Fokker. 31-TET has a slightly less accurate fifth than 12-TET, but provides near-just major thirds, and provides decent matches for harmonics up to at least 13, of which the seventh harmonic is particularly accurate.
In the 20th century, standardized Western pitch and notation practices having been placed on a 12-TET foundation made the quarter tone scale (or 24-TET) a popular microtonal tuning.
29-TET is the lowest number of equal divisions of the octave which produces a better perfect fifth than 12-TET. Its major third is roughly as inaccurate as 12-TET, however it is tuned 14 cents flat rather than 14 cents sharp.
41-TET is the second lowest number of equal divisions which produces a better perfect fifth than 12-TET.
53-TET is better at approximating the traditional just consonances than 12, 19 or 31-TET, but has had only occasional use. Its extremely good perfect fifths make it interchangeable with an extended Pythagorean tuning, but it also accommodates schismatic temperament, and is sometimes used in Turkish music theory. It does not, however, fit the requirements of meantone temperaments which put good thirds within easy reach via the cycle of fifths. In 53-TET the very consonant thirds would be reached instead by strange enharmonic relationships. A consequence of this is that chord progressions like I-vi-ii-V-I won't land you back where you started in 53-TET, but rather one 53-tone step flat (unless the motion by I-vi wasn't by the 5-limit minor third).
Another extension of 12-TET is 72-TET (dividing the semitone into 6 equal parts), which though not a meantone tuning, approximates well most just intonation intervals, even less traditional ones such as 7/4, 9/7, 11/5, 11/6 and 11/7. 72-TET has been taught, written and performed in practice by Joe Maneri and his students (whose atonal inclinations interestingly typically avoid any reference to just intonation whatsoever).
Other equal divisions of the octave that have found occasional use include 14-TET, 15-TET, 16-TET, 17-TET, 19-TET, 22-TET, 34-TET, 46-TET, 48-TET, 99-TET, and 171-TET.
Equal temperaments of non-octave intervals
The equal-tempered version of the Bohlen–Pierce scale consists of the ratio 3:1, 1902 cents, conventionally a perfect fifth wider than an octave, called in this theory a tritave (), and split into a thirteen equal parts. This provides a very close match to justly tuned ratios consisting only of odd numbers. Each step is 146.3 cents (), or ![\sqrt[13]{3}](/2012-wikipedia_en_all_nopic_01_2012/I/f95fb703bef2015ddf200e6ab29058ea.png) .
.
Wendy Carlos created three unusual equal temperaments after a thorough study of the properties of possible temperaments having a step size between 30 and 120 cents. These were called alpha, beta, and gamma. They can be considered as equal divisions of the perfect fifth. Each of them provides a very good approximation of several just intervals.[31] Their step sizes:
- alpha:
![\sqrt[9]{3/2}](/2012-wikipedia_en_all_nopic_01_2012/I/3455a7894e03ef676c063e77089449c1.png) (78.0 cents)
(78.0 cents) - beta:
![\sqrt[11]{3/2}](/2012-wikipedia_en_all_nopic_01_2012/I/93b61ff190f2d59c7f7ee0d73651cfca.png) (63.8 cents)
(63.8 cents) - gamma:
![\sqrt[20]{3/2}](/2012-wikipedia_en_all_nopic_01_2012/I/1bd9c25a83bb351f6dd526b90eb36ee6.png) (35.1 cents)
(35.1 cents)
Alpha and Beta may be heard on the title track of her 1986 album Beauty in the Beast.
See also
- Musical acoustics (the physics of music)
- Music and mathematics
- Microtuner
- Microtonal music
- Piano key frequencies
- Piano tuning
- Semitone
- List of meantone intervals
- Diatonic and chromatic
- Electronic tuner
Notes
- ^ Galilei, V. (1584). Il Fronimo... Dialogo sopra l'arte del bene intavolare. G. Scotto: Venice, ff. 80-89.
- ^ J. Murray Barbour Tuning and Temperament p8 1951 Michigan State University Press
- ^ http://www.philresound.co.uk/page4.htm
- ^ Giacomo Gorzanis, c.1525-c.1575 Intabolatura di liuto. Geneva, 1982
- ^ http://www.library.appstate.edu/music/lute/16index/tspi07a.html
- ^ John Wilson, 26 Preludes, Diapason press (DP49, Utrecht)
- ^ in "English Song, 1600 - 1675, Facsimile of Twenty-six Manuscripts and an Edition of the Texts" vol. 7, Manuscripts at Oxford, Part II. introduction by Elise Bickfoer Jorgens, Garland Publishing Inc., New York and London, 1987
- ^ "Scintille de musica", (Brescia, 1533), p. 132
- ^ Van de Spiegheling der signconst, ed by Rudolf Rasch, The Diapason Press
- ^ Thomas S. Christensen, The Cambridge history of western music theory p205, Cambridge University Press
- ^ Gene Cho, The discovery of musical equal temperament in China and Europe - Page 223, Mellen Press
- ^ Gene Cho, The discovery of musical equal temperament in China and Europe - Page 222, Mellen Press
- ^ Thomas S. Christensen, The Cambridge history of western music theory p207, Cambridge University Press
- ^ Thomas S. Christensen, The Cambridge history of western music theory p78, Cambridge University Press
- ^ "Lutes, Viols, Temperaments" Mark Lindley ISBN 9780521288835
- ^ Vm7 6214
- ^ Owen Henry Jorgensen, Tuning (East Lansing: Michigan State University Press, 1991)
- ^ J. Murray Barbour Tuning and Temperament p55-56, Michigan State University Press 1951
- ^ "有关"七平均律"新文献著作的发现 [Findings of new literatures concerning the hepta - equal temperament]" (in Chinese). Archived from the original on 27 October 2007. http://web.archive.org/web/20071027064731/http://www.wanfangdata.com.cn/qikan/periodical.Articles/ZHONGUOYY/ZHON2004/0404/040425.htm. "'Hepta-equal temperament' in our folk music has always been a controversial issue."
- ^ "七平均律"琐谈--兼及旧式均孔曲笛制作与转调 [abstract of About "Seven- equal- tuning System"]" (in Chinese). http://scholar.ilib.cn/Abstract.aspx?A=xhyyxyxb200102005. "From the flute for two thousand years of the production process, and the Japanese shakuhachi remaining in the production of Sui and Tang Dynasties and the actual temperament, identification of people using the so-called 'Seven Laws' at least two thousand years of history; and decided that this law system associated with the flute law."
- ^ http://uts.cc.utexas.edu/~rhart/papers/quantifying.html Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China Roger Hart Departments of History and Asian Studies, University of Texas, Austin
- ^ The Shorter Science & Civilisation in China, An abridgement by Colin Ronan of Joseph Needham's original text, p385
- ^ Gene J. Cho "The Significance of the Discovery of the Musical Equal Temperament In the Cultural History," http://en.cnki.com.cn/Article_en/CJFDTOTAL-XHYY201002002.htm
- ^ Robert Temple, The Genius of China, p209
- ^ J. Murray Barbour, Tuning and Temperament Michigan University Press, 1951 p7
- ^ [1] "The division of Octave into twelve Semitones, and the transposition of scales have also being discovered by this intelligent and skillful nation" Hermann von Helmholtz On the Sensations of Tone as a Physiological basis for the theory of music , p 258, 3rd edition, Longmans, Green and Co, London, 1895]
- ^ Lau Hanson, Abacus and Practical Mathematics p389 (in Chinese 劳汉生 《珠算与实用数学》 389页)
- ^ Date,name,ratio,cents: from equal temperament monochord tables p55-p78; J. Murray Barbour Tuning and Temperament , Michigan State University Press 1951
- ^ Cordier, Serge. "Le tempérament égal à quintes justes" (in French). Association pour la Recherche et le Développement de la Musique. http://aredem.online.fr/aredem/page_cordier.html. Retrieved 2 June 2010.
- ^ Sethares compares several equal temperament scales in a graph with axes reversed from the axes here. (fig. 4.6, p. 58)
- ^ THREE ASYMMETRIC DIVISIONS OF THE OCTAVE by Wendy Carlos
References
- Burns, Edward M. (1999). "Intervals, Scales, and Tuning", The Psychology of Music second edition. Deutsch, Diana, ed. San Diego: Academic Press. ISBN 0-12-213564-4. Cited:
-
- Ellis, C. (1965). "Pre-instrumental scales", Journal of the Acoustical Society of America, 9, 126-144. Cited in Burns (1999).
- Morton, D. (1974). "Vocal tones in traditional Thai music", Selected reports in ethnomusicology (Vol. 2, p.88-99). Los Angeles: Institute for Ethnomusicology, UCLA. Cited in Burns (1999).
- Haddon, E. (1952). "Possible origin of the Chopi Timbila xylophone", African Music Society Newsletter, 1, 61-67. Cited in Burns (1999).
- Kunst, J. (1949). Music in Java (Vol. II). The Hague: Marinus Nijhoff. Cited in Burns (1999).
- Hood, M. (1966). "Slendro and Pelog redefined", Selected Reports in Ethnomusicology, Institute of Ethnomusicology, UCLA, 1, 36-48. Cited in Burns (1999).
- Temple, Robert K. G. (1986)."The Genius of China". ISBN 0-671-62028-2. Cited in Burns (1999).
- Tenzer, (2000). Gamelan Gong Kebyar: The Art of Twentieth-Century Balinese Music. ISBN 0-226-79281-1 and ISBN 0-226-79283-8. Cited in Burns (1999).
- Boiles, J. (1969). "Terpehua though-song", Ethnomusicology, 13, 42-47. Cited in Burns (1999).
- Wachsmann, K. (1950). "An equal-stepped tuning in a Ganda harp", Nature (Longdon), 165, 40. Cited in Burns (1999).
- Cho, Gene Jinsiong. (2003). The Discovery of Musical Equal Temperament in China and Europe in the Sixteenth Century. Lewiston, NY: Edwin Mellen Press.
- Jorgensen, Owen. Tuning. Michigan State University Press, 1991. ISBN 0-87013-290-3
- Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale (2nd ed. ed.). London: Springer-Verlag. ISBN 1852337974.
- Surjodiningrat, W., Sudarjana, P.J., and Susanto, A. (1972) Tone measurements of outstanding Javanese gamelans in Jogjakarta and Surakarta, Gadjah Mada University Press, Jogjakarta 1972. Cited on http://web.telia.com/~u57011259/pelog_main.htm, accessed May 19, 2006.
- Stewart, P. J. (2006) "From Galaxy to Galaxy: Music of the Spheres" [2]
- Khramov, Mykhaylo. "Approximation of 5-limit just intonation. Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave", Proceedings of the International Conference SIGMAP-2008, 26–29 July 2008, Porto, pp. 181–184, ISBN 978-989-8111-60-9
External links
- "An Introduction to Historical Tunings" by Kyle Gann, KyleGann.com.
- Huygens-Fokker Foundation Centre for Microtonal Music
- "Uncertainty Principle for Temperament" by Iori Fujita, Music of Sacred Temperament.
- A.Orlandini: Music Acoustics
- "Temperament" from A supplement to Mr. Chambers's cyclopædia (1753)
- "Tuned Piano", WebMetronome - a web piano tuned to equal temperament.
- "12TET Frequency Table Maker" - Creates a frequency table (Hz.) for all 12TET pitches
- "HANDBOOK OF ACOUSTICS - online book" Brief description of Scheibler's tonometer
- Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante Libreria Editrice
- "Fractal Microtonal Music", Jim Kukula.
|
|||||||||||||||||||||||||
![\sqrt [24]{2}](/2012-wikipedia_en_all_nopic_01_2012/I/f04d26d2e0e11ae8ee02d77ed0d8e0dc.png)
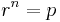
![r=\sqrt[n]{p}](/2012-wikipedia_en_all_nopic_01_2012/I/2c9a0e8837733d67c15a5987225272ac.png)
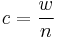
![P_n=P_a(\sqrt[12]{2})^{(n-a)}](/2012-wikipedia_en_all_nopic_01_2012/I/03577134f71db33100e549628947a723.png)
![P_{40}=440(\sqrt[12]{2})^{(40-49)}\approx 261.626~\text{Hz}](/2012-wikipedia_en_all_nopic_01_2012/I/3dfb15ef114078b74b7b8469371068be.png)