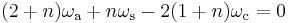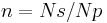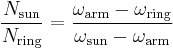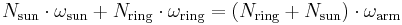Epicyclic gearing
Epicyclic gearing or planetary gearing is a gear system consisting of one or more outer gears, or planet gears, revolving about a central, or sun gear. Typically, the planet gears are mounted on a movable arm or carrier which itself may rotate relative to the sun gear. Epicyclic gearing systems also incorporate the use of an outer ring gear or annulus, which meshes with the planet gears. Planetary gears (or epicyclic gears) are typically classified as simple and compound planetary gears. Simple planetary gears have one sun, one ring, one carrier, and one planet set. Compound planetary gears involve one or more of the following three types of structures: meshed-planet (there are at least two more planets in mesh with each other in each planet train), stepped-planet (there exists a shaft connection between two planets in each planet train), and multi-stage structures (the system contains two or more planet sets). Compared to simple planetary gears, compound planetary gears have the advantages of larger reduction ratio, higher torque-to-weight ratio, and more flexible configurations.
The axes of all gears are usually parallel, but for special cases like pencil sharpeners they can be placed at an angle, introducing elements of bevel gear (see below). Further, the sun, planet carrier and annulus axes are usually concentric.
Contents |
Gear ratio
The gear ratio in an epicyclic gearing system is somewhat non-intuitive, particularly because there are several ways in which an input rotation can be converted into an output rotation. The three basic components of the epicyclic gear are:
- Sun: The central gear
- Planet carrier: Holds one or more peripheral planet gears, all of the same size, meshed with the sun gear
- Annulus: An outer ring with inward-facing teeth that mesh with the planet gear or gears
In many epicyclic gearing systems, one of these three basic components is held stationary; one of the two remaining components is an input, providing power to the system, while the last component is an output, receiving power from the system. The ratio of input rotation to output rotation is dependent upon the number of teeth in each gear, and upon which component is held stationary.
In other systems, such as hybrid vehicle transmissions, two of the components are used as inputs with the third providing output relative to the two inputs.[1]
In one arrangement, the planetary carrier (green) is held stationary, and the sun gear (yellow) is used as input. In this case, the planetary gears simply rotate about their own axes (ie, spin) at a rate determined by the number of teeth in each gear. If the sun gear has Ns teeth, and each planet gear has Np teeth, then the ratio is equal to -Ns/Np. For instance, if the sun gear has 24 teeth, and each planet has 16 teeth, then the ratio is -24/16, or -3/2; this means that one clockwise turn of the sun gear produces 1.5 counterclockwise turns of each of the planet gear(s) about its axis.
This rotation of the planet gears can in turn drive the annulus (not depicted in diagram), in a corresponding ratio. If the annulus has Na teeth, then the annulus will rotate by Np/Na turns for each turn of the planet gears. For instance, if the annulus has 64 teeth, and the planets 16, one clockwise turn of a planet gear results in 16/64, or 1/4 clockwise turns of the annulus. Extending this case from the one above:
- One turn of the sun gear results in
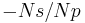 turns of the planets
turns of the planets - One turn of a planet gear results in
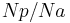 turns of the annulus
turns of the annulus
So, with the planetary carrier locked, one turn of the sun gear results in 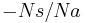 turns of the annulus.
turns of the annulus.
The annulus may also be held fixed, with input provided to the planetary gear carrier; output rotation is then produced from the sun gear. This configuration will produce an increase in gear ratio, equal to 1+Na/Ns.
These are all described by the equation:
where n is the form factor of the planetary gear, defined by:
If the annulus is held stationary and the sun gear is used as the input, the planet carrier will be the output. The gear ratio in this case will be 1/(1+Na/Ns). This is the lowest gear ratio attainable with an epicyclic gear train. This type of gearing is sometimes used in tractors and construction equipment to provide high torque to the drive wheels.
In bicycle hub gears, the sun is usually stationary, being keyed to the axle or even machined directly onto it. The planetary gear carrier is used as input. In this case the gear ratio is simply given by (Ns+Na)/Na. The number of teeth in the planet gear is irrelevant.
Compound planetary gears
"Compound planetary gear" is a general concept and it refers to any planetary gears involve one or more of the following three types of structures: meshed-planet (there are at least two more planets in mesh with each other in each planet train), stepped-planet (there exists a shaft connection between two planets in each planet train), and multi-stage structures (the system contains two or more planet sets).
Some designs use "stepped-planet" which have two differently-sized gears on either end of a common casting. The large end engages the sun, while the small end engages the annulus. This may be necessary to achieve smaller step changes in gear ratio when the overall package size is limited. Compound planets have "timing marks" (or "relative gear mesh phase" in technical term). The assembly conditions of compound planetary gears are more restrictive then simple planetary gears, and they must be assembled in the correct initial orientation relative to each other, or their teeth will not simultaneously engage the sun and annulus at opposite ends of the planet, leading to very rough running and short life. Compound planetary gears can easily achieve larger transmission ratio with equal or smaller volume. For example, compound planets with teeth in a 2:1 ratio with a 50T annulus would give the same effect as a 100T annulus, but with half the actual diameter.
More planet and sun gear units can be placed in series in the same annulus housing (where the output shaft of the first stage becomes the input shaft of the next stage) providing a larger (or smaller) gear ratio. This is the way some automatic transmissions work.
During World War II, a special variation of epicyclic gearing was developed for portable radar gear, where a very high reduction ratio in a small package was needed. This had two outer annular gears, each half the thickness of the other gears. One of these two annular gears was held fixed and had one tooth fewer than did the other. Therefore, several turns of the "sun" gear made the "planet" gears complete a single revolution, which in turn made the rotating annular gear rotate by a single tooth.
Calculating the output from the input
It is first drawn simplified as the sun, a single planet, the annulus, and an arm holding the planet (a simple planetary gear). Any gear can be the input or output, including the arm.
Now, put in the known values and solve for  ring:
ring:
or you can use the other form of this equation:
where N is the number of teeth, 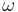 is angular velocity of the element (sun, arm, or ring). Since the angular velocity and rpm are directly proportional, you can use rpm instead.
is angular velocity of the element (sun, arm, or ring). Since the angular velocity and rpm are directly proportional, you can use rpm instead.
However, if the arm is the input or output, say the ring is the output/input instead and reverse the direction (since if the arm moves a certain speed relative to the ring, the ring moves that same speed the other way relative to the arm, and obviously the arm does not have a tooth count to plug in)
To derive this, just imagine the arm is locked, and calculate the gear ratio 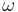 ring /
ring / 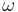 sun = Nsun / Nring, then unlock the arm. From the arms reference frame the ratio is always Nsun/Nring, but from your frame all the speeds are increased by the angular velocity of the arm. So to write this relative relationship, you arrive at the equation from above.
sun = Nsun / Nring, then unlock the arm. From the arms reference frame the ratio is always Nsun/Nring, but from your frame all the speeds are increased by the angular velocity of the arm. So to write this relative relationship, you arrive at the equation from above.
Also, make sure Nsun+2Nplanet=Nring where N is the number of teeth. This simply says that the gears will fit, since N is directly proportional to diameter.
Formulas for calculating gear ratios
| Name | Number of teeth | Speed |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
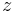 |
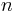 |
 |
 |
 |
 |
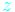 |
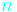 |
| Sketch | Output speed | Sketch | Output speed | Sketch | Output speed | Sketch | Output speed |
|---|---|---|---|---|---|---|---|
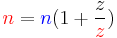 |
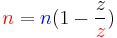 |
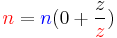 |
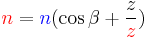 |
||||
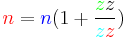 |
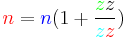 |
 |
 |
||||
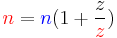 |
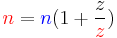 |
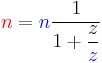 |
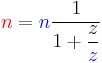 |
||||
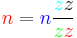 |
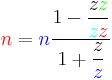 |
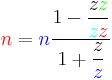 |
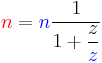 |
||||
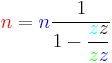 |
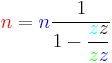 |
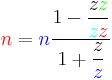 |
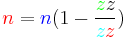 |
||||
![{\color{red} n} = {\color{blue} n} \left[1-\left( \frac {\color{magenta} n} {\color{blue} n} -1 \right) \frac{\color{magenta}z} {\color{red}z}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/a65b1f2476b954b2d6fa6294da8cab05.png) |
![{\color{red} n} = {\color{blue} n} \left[1-\left( \frac {\color{magenta} n} {\color{blue} n} -1 \right) \frac{\color{magenta}z} {\color{red}z}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/a65b1f2476b954b2d6fa6294da8cab05.png) |
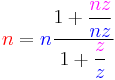 |
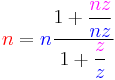 |
Advantages and disadvantages
Advantages of planetary gears over parallel axis gears include high power density, large reduction in a small volume, multiple kinematic combinations, pure torsional reactions, and coaxial shafting. Disadvantages include high bearing loads, inaccessibility, and design complexity.[3][4] The planetary gearbox arrangement is an engineering design that offers many advantages over traditional gearbox arrangements. One advantage is its unique combination of both compactness and outstanding power transmission efficiencies. A typical efficiency loss in a planetary gearbox arrangement is only 3% per stage. This type of efficiency ensures that a high proportion of the energy being input is transmitted through the gearbox, rather than being wasted on mechanical losses inside the gearbox.
Another advantage of the planetary gearbox arrangement is load distribution. Because the load being transmitted is shared between multiple planets, torque capability is greatly increased. The more planets in the system, the greater load ability and the higher the torque density.
The planetary gearbox arrangement also creates greater stability due to the even distribution of mass and increased rotational stiffness.
References
- ^ John M. Miller (2005-10-26). "Hybrid electric vehicle propulsion system architectures of the e-CVT type". IEEE Transactions on Power Electronics 21 (3): 756–767. doi:10.1109/TPEL.2006.872372. http://www.greenhybrid.com/discuss/attachments/f13/578-dual-mode-vs-synergy-miller_hev-propulsion-system-architectures.pdf.
- ^ Pattantyús Gépész- és Villamosmérnökök Kézikönyve 3. tom. Műszaki Könyvkiadó, Budapest, 1961. p.632.
- ^ Lynwander, P., 1983, Gear Drive Systems: Design and Application. Marcel Dekker, New York
- ^ Smith, J. D., 1983, Gears and Their Vibration: A Basic Approach to Understanding Gear Noise. Marcel Dekker, New York and MacMillan, London
5. Guo, Y., Analytical Study On Compound Planetary Gear Dynamics, The Ohio State University, 2011. (http://etd.ohiolink.edu/view.cgi?acc_num=osu1312289370)
6. Guo, Y., and Parker, R. G. “Sensitivity of General Compound Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters”. Journal of Vibration and Acoustics, 132(1):1–13, 2010. (http://link.aip.org/link/?JVACEK/132/011006/1)
7. Guo, Y., and Parker, R. G. “Purely Rotational Model and Vibration Modes of Compound Planetary Gears”. Mechanism and Machine Theory, 45:365–377, 2010. (http://www.sciencedirect.com/science/article/pii/S0094114X09001578)
8. Guo, Y., and Parker, R. G. “Analytical Determination of Mesh Phase Relations in General Compound Planetary Gears”. Mechanism and Machine Theory, 2011. (http://www.sciencedirect.com/science/article/pii/S0094114X11001443)
9. D. R. Kiracofe and R. G. Parker. Structured vibration modes of general compound planetary gear systems. Journal of Vibration and Acoustics, 129(1):1–16, February 2007.
10. A. Kahraman. Free torsional vibration characteristics of compound planetary gear sets. Mechanism and Machine Theory, 36:953–971, 2001.
Gallery
See also
- Continuously variable transmission (CVT)
- Cycloidal drive
- Epicycloid
- Ford Model T
- NuVinci gearing
- Ravigneaux planetary gearset
- Rohloff Speedhub, 14-ratio bicycle hub gearbox
- Antikythera mechanism, ancient mechanical astronomical computer
External links
- Parvalux have an animated 3D movie on their homepage of a 2-stage planetary gearhead in motion
- Kinematic Models for Design Digital Library (KMODDL)
Movies and photos of hundreds of working mechanical-systems models at Cornell. - "Animation of Epicyclic gearing"
- The "Power Split Device"
- The "Interactive Planetary Gearset tutorial"
- Interactive Prius planetary gear example" another one
- [1] Purely rotational model and vibration modes of compound planetary gears
- [2] Free torsional vibration characteristics of compound planetary gear sets
- [3] Structured Vibration Modes of General Compound Planetary Gear Systems
- [4] Sensitivity of General Compound Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters
- [5] Analytical determination of mesh phase relations in general compound planetary gears
- [6] Ph.D. Dissertation on Compound Planetary Gears
|
||||||||||||||||||||