Elongated square cupola

Elongated square cupola
Type Johnson
J18 - J19 - J20
Faces 4 triangles
1+3.4 squares
1 octagon
Edges 36
Vertices 20
Vertex configuration 8(42.8)
4+8(3.43)
Symmetry group C4v
Dual polyhedron -
Properties convex
Net

In geometry, the elongated square cupola is one of the Johnson solids (J19). As the name suggests, it can be constructed by elongating a square cupola (J4) by attaching an octagonal prism to its base. The solid can be seen as a rhombicuboctahedron with its "lid" (another square cupola) removed.

The 92 Johnson solids were named and described by Norman Johnson in 1966.

Contents

Formulae

The following formulae for volume, surface area and circumradius can be used if all faces are regular, with edge length a:[1]

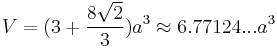
V=(3%2B\frac{8\sqrt{2}}{3})a^3\approx6.77124...a^3

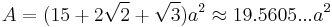
A=(15%2B2\sqrt{2}%2B\sqrt{3})a^2\approx19.5605...a^2

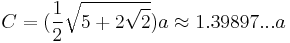
C=(\frac{1}{2}\sqrt{5%2B2\sqrt{2}})a\approx1.39897...a

Dual polyhedron

The dual of the elongated square cupola has 20 faces: 8 isoceles triangles, 4 kites, 8 quadrilaterals.

Dual elongated square cupola Net of dual

References

  1. ^ Stephen Wolfram, "Elongated square cupola" from Wolfram Alpha. Retrieved July 22, 2010.

External links