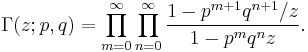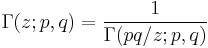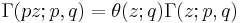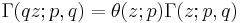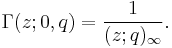Elliptic gamma function
In mathematics, the elliptic gamma function is a generalization of the q-Gamma function, which is itself the q-analog of the ordinary Gamma function. It is closely related to a function studied by Jackson (1905), and can be expressed in terms of the triple gamma function. It is given by
It obeys several identities:
and
where θ is the q-theta function.
When 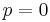 , it essentially reduces to the infinite q-Pochhammer symbol:
, it essentially reduces to the infinite q-Pochhammer symbol:
References
- Jackson, F. H. (1905), "The Basic Gamma-Function and the Elliptic Functions", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (The Royal Society) 76 (508): 127–144, ISSN 0950-1207, JSTOR 92601
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, ISBN 978-0-521-83357-8, MR2128719
- Ruijsenaars, S. N. M. (1997), "First order analytic difference equations and integrable quantum systems", Journal of Mathematical Physics 38 (2): 1069–1146, doi:10.1063/1.531809, ISSN 0022-2488, MR1434226