Elitzur–Vaidman bomb tester

Quantum mechanics
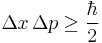\Delta x\, \Delta p \ge \frac{\hbar}{2}
Introduction
Glossary · History
Experiments
Bell's inequality · Davisson–Germer
Delayed choice quantum eraser
Double-slit · Elitzur–Vaidman
Popper · Quantum eraser
Schrödinger's cat · Stern–Gerlach
Wheeler's delayed choice

In physics, the Elitzur–Vaidman bomb-testing problem is a thought experiment in quantum mechanics, first proposed by Avshalom Elitzur and Lev Vaidman in 1993.[1] An actual experiment demonstrating the solution was constructed and successfully tested by Anton Zeilinger, Paul Kwiat, Harald Weinfurter, and Thomas Herzog in 1994.[2] It employs a Mach–Zehnder interferometer for ascertaining whether a measurement has taken place. It was chosen by the New Scientist magazine as one of the seven wonders of quantum world.[3]

Contents

Problem

Consider a collection of bombs, some of which are duds. Suppose these bombs carry a certain perfect property: usable bombs have a photon-triggered sensor which will absorb a photon and detonate. Dud bombs have a malfunctioning sensor which will not interfere with any photons.[4] The problem is how to separate at least some of the usable bombs from the duds. A bomb sorter could accumulate dud bombs by attempting to detonate each one. Unfortunately, this naive process destroys all the usable bombs.

Solution

A solution is for the sorter to use a mode of observation known as counterfactual measurement, which relies on properties of quantum mechanics.[5]

Start with a Mach–Zehnder interferometer and a light source which emits single photons. When a photon emitted by the light source reaches a half-silvered plane mirror, it has equal chances of passing through or reflecting.[6] On one path, place a bomb (B) for the photon to encounter. If the bomb is working, then the photon is absorbed and triggers the bomb. If the bomb is non-functional, the photon will pass through the dud bomb unaffected.

When a photon's state is non-deterministically altered, such as interacting with a half-silvered mirror where it non-deterministically passes through or is reflected, the photon undergoes quantum superposition, whereby it takes on all possible states and can interact with itself. This phenomenon continues until an 'observer' (detector) interacts with it, causing the wave function to collapse and returning the photon to a deterministic state.

Step-by-step explanation

If the bomb is a dud:

If the bomb is usable:

Thus we can state that if any photons are detected at (C), there must have been a working detector at (B) – the bomb position.

With this process, 25% of the usable bombs can be identified as usable without being consumed.[1] whilst 50% of the usable bombs will be consumed and 25% remain 'unknown'. By repeating the process with the 'unknowns', the ratio of surviving, identified, usable bombs approaches 33% of the initial population of usable bombs. See Experiments section below for a modified experiment that can identify the usable bombs with a yield rate approaching 100%.

Many-worlds interpretation

One conceptual way to understand this phenomenon is through the Everett many-worlds interpretation. The superposition behaviour is analogous to having parallel worlds for all possible states of the photon. Therefore, when a photon encounters a half-silvered mirror, in one world it passes through, and in another world it reflects off the mirror. These two worlds are completely separate except for the particle in superposition. The photon that passes through the mirror in one world may interact with the photon that reflected off the mirror in the other world. The photons may continue to interact with each other until an observer from one world measures the photon's state. This produces the incredible but necessarily counterfactual results of the gedanken (thought experiment).

See also: Many-worlds interpretation#Weak coupling

Experiments

In 1994, Anton Zeilinger, Paul Kwiat, Harald Weinfurter, and Thomas Herzog actually performed an equivalent of the above experiment, proving interaction-free measurements are indeed possible.[2]

In 1996, Kwiat et al. devised a method, using a sequence of polarising devices, that efficiently increases the yield rate to a level arbitrarily close to one. The key idea is to split a fraction of the photon beam into a large number of beams of very small amplitude, and reflect all of them off the mirror, recombining them with the original beam afterwards.[7] ( See also http://www.nature.com/nature/journal/v439/n7079/full/nature04523.html#B1 .) It can also be argued that this revised construction is simply equivalent to a resonant cavity and the result looks much less shocking in this language. See Watanabe and Inoue (2000).

This experiment is philosophically significant because it determines the answer to a counterfactual question: "What would happen were the photon to pass through the bomb sensor?". The answer is either: "the bomb works, the photon was observed, and the bomb will explode", or "the bomb is a dud, the photon was not observed, and the photon passes through unimpeded". If we were actually to perform the measurement, any bomb would actually explode. But here the answer to the question "what would happen" is determined without the bomb going off. This provides an example of an experimental method to answer a counterfactual question.

See also

References

  1. ^ a b Elitzur & Vaidman 1993
  2. ^ a b Paul Kwiat 1994
  3. ^ Seven wonders of the quantum world, newscientist.com
  4. ^ Can Schrodinger's Cat Collapse the Wavefunction?, Keith Bowden 1997
  5. ^ Keith Bowden (k.bowden@physics.bbk.ac.uk)
  6. ^ David Harrison
  7. ^ Kwiat: Tao of Interaction-Free Measurements

Further reading