Elementary matrix

In mathematics, an elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices. Left multiplication (pre-multiplication) by an elementary matrix represents elementary row operations, while right multiplication (post-multiplication) represents elementary column operations.

In algebraic K-theory, "elementary matrices" refers only to the row-addition matrices.

Contents

Use in solving systems of equations

Elementary row operations do not change the solution set of the system of linear equations represented by a matrix, and are used in Gaussian elimination (respectively, Gauss-Jordan elimination) to reduce a matrix to row echelon form (respectively, reduced row echelon form).

The acronym "ERO" is commonly used for "elementary row operations".

Elementary row operations do not change the kernel of a matrix (and hence do not change the solution set), but they do change the image. Dually, elementary column operations do not change the image, but they do change the kernel.

There are three types of (n x n) elementary matrices: 1) Permutation Matrix 2) Diagonal Matrix 3) Unipotent Matrix

Operations

There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):

Row switching
A row within the matrix can be switched with another row.
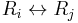
R_i \leftrightarrow R_j
Row multiplication
Each element in a row can be multiplied by a non-zero constant.
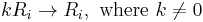
kR_i \rightarrow R_i,\ \mbox{where } k \neq 0
Row addition
A row can be replaced by the sum of that row and a multiple of another row.
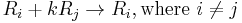
R_i %2B kR_j \rightarrow R_i, \mbox{where } i \neq j

The elementary matrix for any row operation is obtained by executing the operation on an identity matrix.

Row-switching transformations

This transformation, Tij, switches all matrix elements on row i with their counterparts on row j. The matrix resulting in this transformation is obtained by swapping row i and row j of the identity matrix.

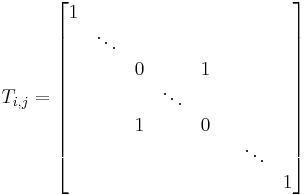
T_{i,j} = \begin{bmatrix} 1 & & & & & & & \\ & \ddots & & & & & & \\ & & 0 & & 1 & & \\ & & & \ddots & & & & \\ & & 1 & & 0 & & \\ & & & & & & \ddots & \\ & & & & & & & 1\end{bmatrix}\quad
That is, Tij is the matrix produced by exchanging row i and row j of the identity matrix.

Properties

  • The inverse of this matrix is itself: Tij−1=Tij.
  • Since the determinant of the identity matrix is unity, det[Tij] = −1. It follows that for any conformable square matrix A: det[TijA] = −det[A].

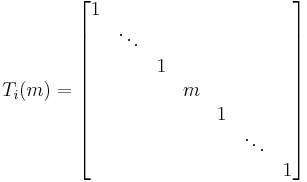
Row-multiplying transformations

This transformation, Ti(m), multiplies all elements on row i by m where m is non zero. The matrix resulting in this transformation is obtained by multiplying all elements of row i of the identity matrix by m.

T_i(m) = \begin{bmatrix} 1 & & & & & & \\ & \ddots & & & & & \\ & & 1 & & & & \\ & & & m & & & \\ & & & & 1 & & \\ & & & & & \ddots & \\ & & & & & & 1\end{bmatrix}\quad

Properties

  • The inverse of this matrix is: Ti(m)−1 = Ti(1/m).
  • The matrix and its inverse are diagonal matrices.
  • det[Ti(m)] = m. Therefore for a conformable square matrix A: det[Ti(m)A] = m det[A].

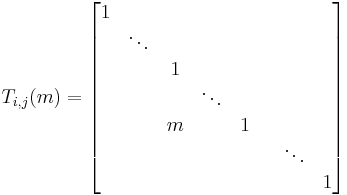
Row-addition transformations

This transformation, Tij(m), adds row j multiplied by m to row i. The matrix resulting in this transformation is obtained by taking row j of the identity matrix, and adding it m times to row i.

T_{i,j}(m) = \begin{bmatrix} 1 & & & & & & & \\ & \ddots & & & & & & \\ & & 1 & & & & & \\ & & & \ddots & & & & \\ & & m & & 1 & & \\ & & & & & & \ddots & \\ & & & & & & & 1\end{bmatrix}

These are also called shear mappings or transvections.

Properties

  • Tij(m)−1 = Tij(−m) (inverse matrix).
  • The matrix and its inverse are triangular matrices.
  • det[Tij(m)] = 1. Therefore, for a conformable square matrix A: det[Tij(1)A] = det[A].
Row-addition transforms satisfy the Steinberg relations.

See also

References

See also: Linear algebra#Further reading