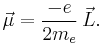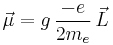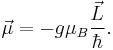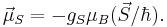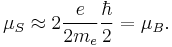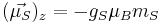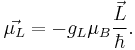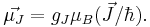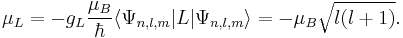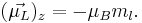Electron magnetic dipole moment

In atomic physics, the electron magnetic dipole moment is the magnetic moment of an electron caused by its intrinsic property of spin.

1 Magnetic moment of an electron
2 Spin magnetic dipole moment
3 Orbital magnetic dipole moment
4 Total magnetic dipole moment
5 Example: hydrogen atom
6 See also
7 Notes

Magnetic moment of an electron

The electron is a charged particle. Its angular momentum comes from two types of rotation: spin and orbital motion. From classical electrodynamics, a rotating electrically charged body creates a magnetic dipole with magnetic poles of equal magnitude but opposite polarity. This analogy holds as an electron indeed behaves like a tiny bar magnet. One consequence is that an external magnetic field exerts a torque on the electron magnetic moment depending on its orientation with respect to the field.

If the electron is visualized as a classical charged particle literally rotating about an axis with angular momentum 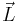$\vec{L}$ , its magnetic dipole moment $\vec{\mu}$ is given by:

$\vec{\mu} = \frac{-e}{2m_e}\, \vec{L}.$

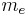Here the charge is − $e$ , where $e$ is the elementary charge. The mass is the electron rest mass $m_e$ . Note that the angular momentum 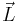$\vec{L}$ in this equation may be the spin angular momentum, the orbital angular momentum, or the total angular momentum. It turns out the classical result is off by a proportional factor for the spin magnetic moment. As a result, the classical result is corrected by multiplying it with a correction factor.

$\vec{\mu} = g \, \frac{-e}{2m_e}\, \vec{L}$

The dimensionless correction factor g is known as the g-factor. Finally, it is customary to express the magnetic moment in terms of the Planck constant and the Bohr magneton:

$\vec{\mu} = -g \mu_B \frac{\vec{L}}{\hbar}.$

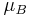Here $\mu_{B}$ is the Bohr magneton and 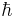$\hbar\,$ is the reduced Planck constant.

Spin magnetic dipole moment

The spin magnetic moment is intrinsic for an electron.^[1] It is:

$\vec{\mu}_S=-g_S \mu_B (\vec{S}/\hbar).$

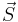Here $\vec{S}$ is the electron spin angular momentum. The spin g-factor is approximately two: 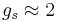$g_s\approx2$ . The magnetic moment of an electron is approximately twice what it should be in classical mechanics. The factor of two difference implies that the electron appears to be twice as effective in producing a magnetic moment as the corresponding classical charged body.

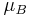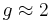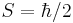The spin magnetic dipole moment is approximately one $\mu_{B}$ because $g\approx 2$ and the electron is a spin one-half particle: $S=\hbar/2$ .

$\mu_S\approx 2\frac{e}{2m_e}\frac{\hbar}{2}=\mu_B.$

The z component of the electron magnetic moment is:

$(\vec{\mu_S})_z=-g_S \mu_B m_S$

where m_S is the spin quantum number. Note that $\vec{\mu}$ is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum.

The spin g-factor 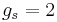$g_s=2$ comes from the Dirac equation, a fundamental equation connecting the electron's spin with its electromagnetic properties. Reduction of the Dirac equation for an electron in a magnetic field to its non-relativistic limit yields the Schrödinger equation with a correction term which takes account of the interaction of the electron's intrinsic magnetic moment with the magnetic field giving the correct energy.

For the electron spin, the most accurate value for the spin g-factor has been experimentally determined to have the value 2.00231930419922 ± (1.5 × 10⁻¹²).^[2] Note that it is only two thousandths larger than the value from Dirac equation. The small correction is known as the anomalous magnetic dipole moment of the electron; it arises from the electron's interaction with virtual photons in quantum electrodynamics. In fact, one famous triumph of the Quantum Electrodynamics theory is the accurate prediction of the electron g-factor. The most accurate value for the electron magnetic moment is -928.476377 × 10⁻²⁶ ± 0.000023 × 10⁻²⁶ J/T.^[3]

Orbital magnetic dipole moment

The revolution of an electron around an axis through another object, such as the nucleus, gives rise to the orbital magnetic dipole moment. Suppose that the angular momentum for the orbital motion is 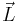$\vec{L}$ . Then the orbital magnetic dipole moment is:

$\vec{\mu_L}=-g_L\mu_B \frac{\vec{L}}{\hbar}.$

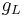Here $g_L$ is the electron orbital g-factor and 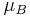$\mu_B$ is the Bohr magneton. The value of 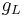$g_L$ is exactly equal to one, by a quantum-mechanical argument analogous to the derivation of the classical gyromagnetic ratio.

Total magnetic dipole moment

The total magnetic dipole moment resulting from both spin and orbital angular momenta of an electron is related to the total angular momentum J = L+S by:

$\vec{\mu_J}=g_J \mu_B (\vec{J}/\hbar).$

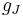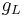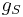The g-factor $g_J$ is known as the Landé g-factor, which can be related to $g_L$ and $g_S$ by quantum mechanics. See the article on Landé g-factor.

Example: hydrogen atom

For a hydrogen atom, an electron occupying the atomic orbital 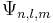$\Psi_{n,l,m}$ , the magnetic dipole moment is given by:

$\mu_L=-g_L\frac{\mu_B}{\hbar}\langle\Psi_{n,l,m}|L|\Psi_{n,l,m}\rangle=-\mu_B\sqrt{l(l%2B1)}.$

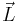Here $\vec{L}$ is the orbital angular momentum, 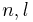$n, l$ and $m$ are the principal, azimuthal and magnetic quantum numbers. The z-component of the orbital magnetic dipole moment for an electron with a magnetic quantum number m_l is given by:

$(\vec{\mu_L})_z=-\mu_B m_l.\,$

Notes

^ A. Mahajan and A. Rangwala. Electricity and Magnetism, p. 419 (1989). Via Google Books.
^ http://physics.nist.gov/cgi-bin/cuu/Value?eqae|search_for=electron+magnetic+moment
^ http://physics.nist.gov/cgi-bin/cuu/Value?muem|search_for=magnetic+moment+electron