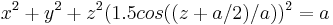Oval
In technical drawing, an oval (from Latin ovum, 'egg') is a figure constructed from two pairs of arcs, with two different radii (see image on the right). The arcs are joined at a point, in which lines tangential to both joining arcs lie on the same line, thus making the joint smooth. Any point of an oval belongs to an arc with a constant radius (shorter or longer), whereas in an ellipse the radius is continuously changing.
Contents |
Oval in geometry
In geometry, an oval or ovoid is any curve resembling an egg or an ellipse, but not an ellipse. Unlike other curves, the term 'oval' is not well-defined and many distinct curves are commonly called ovals. These curves have in common that:
- they are differentiable (smooth-looking), simple (not self-intersecting), convex, closed, plane curves;
- their shape does not depart much from that of an ellipse, and
- there is at least one axis of symmetry.
The word ovoidal refers to the characteristic of being an ovoid. An ovoid is the surface generated by rotating an oval curve about one of its axes of symmetry.
Other examples of ovals described elsewhere include:
Egg shape
The shape of an egg is approximately half of each prolate (long) and is a roughly spherical (potentially even slightly oblate/short) ellipsoid joined at the equator, sharing a principal axis of rotational symmetry, as illustrated above. Although the term egg-shaped usually implies a lack of reflection symmetry across the equatorial plane, it may also refer to true prolate ellipsoids. It can also be used to describe the 2-dimensional figure that, revolved around its major axis, produces the 3-dimensional surface. Refer to the following equation for an approximation of a 3D egg where a is any positive constant:
Projective planes
In the theory of projective planes, oval is used to mean a set of n + 1 points in a projective plane of order n, with no 3 on any line. See oval (projective plane).
In common English
In common speech "oval" means a shape rather like an egg or an ellipse, and it may be two-dimensional or three-dimensional. It also often refers to a figure that resembles two semicircles joined by a rectangle, like a cricket infield or oval racing track. This is more correctly, although archaically, described as oblong.[1] Sometimes it can even refer to any rectangle with rounded corners.
See also
- Squoval
- Vesica piscis - a pointed oval
References
- ^ "Oblong". Oxford English Dictionary. 1933. "A adj. 1. Elongated in one direction (usually as a deviation from an exact square or circular form): having the chief axis considerably longer than the transverse diameter"