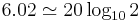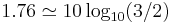Effective number of bits

Effective number of bits (ENOB) is a measure of the quality of a digitised signal. The resolution of a digital-to-analog or analog-to-digital converter (DAC or ADC) is commonly specified by the number of bits used to represent the analog value, in principle giving 2N signal levels for an N-bit signal. However, all real signals contain a certain amount of noise. If the converter is able to represent signal levels below the system noise floor, the lower bits of the digitised signal only represent system noise and do not contain useful information. ENOB specifies the number of bits in the digitised signal above the noise floor. Often ENOB is used as a quality measure also for other blocks like sample-and-hold amplifiers. This way also analog blocks can be easily included to signal-chain calculations as the total ENOB of a chain of blocks is usually below the ENOB of the worst block.

Contents

Definition

An often used definition for ENOB is[1]

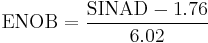\mathrm{ENOB} = \frac{\mathrm{SINAD}-1.76}{6.02},

where all values are given in dB, and

This definition compares the SINAD of an ideal ADC or DAC with a word length of ENOB bits with the SINAD of the ADC or DAC being tested.

Example

The following are measurements of a 3-bit unipolar D/A converter with reference voltage Vref = 8 V:

Digital Input 000 001 010 011 100 101 110 111
Analog Output (V) -0.01 1.03 2.02 2.96 3.95 5.02 6.00 7.08

The offset error in this case is -0.01 V or -0.01 LSB as 1 V = 1 LSB in this example. The gain error is

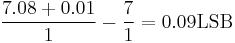\frac{7.08%2B0.01}{1}-\frac{7}{1} = 0.09 \mathrm{LSB}.

Correcting the offset and gain error, we obtain the following list of measurements:

This allows the INL and DNL to be calculated:

The absolute and relative accuracy can now be calculated. In this case, the ENOB absolute accuracy is calculated using the largest absolute deviation D, in this case 0.08 V:

D = \frac{V_{ref}}{2^\mathrm{ENOB}} \Rightarrow \mathrm{ENOB}_{abs} = 6.64 \ \mathrm{bits}

The effective number of bits relative accuracy is calculated using the largest relative (INL) deviation d, in this case 0.09 V.

d = \frac{V_{ref}}{2^\mathrm{ENOB}} \Rightarrow \mathrm{ENOB}_{rel} = 6.47 \ \mathrm{bits}

For this kind of ENOB calculation, note that the effective number of bits can be larger or smaller than the actual number of bits. When the ENOB is smaller than the ANOB, this means that some of the least significant bits of the result are inaccurate. However, one can also argue that the ENOB can never be larger than the ANOB, because you always have to add the quantization error of an ideal converter which is +-0.5 LSB. Different designers may use different definitions of ENOB!

See also

Notes

  1. ^ 6.02 \simeq 20 \log_{10}2
  2. ^ 1.76 \simeq 10 \log_{10}( 3/2 )[2]

References

  1. ^ Kester 2009, p. 5, Equation 1.
  2. ^ Eq. 2.8 in "Design of multi-bit delta-sigma A/D converters", Yves Geerts, Michiel Steyaert, Willy M. C. Sansen, 2002.

External links

Noise (in physics and telecommunications)
General
Noise in...
Class of noise
Engineering terms
Ratios
Related topics